题目内容
12. 如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由折叠的性质和等腰三角形的性质可得,∠PDE=∠PED=∠BPE=∠APB,由平行线的性质,可得∠APB=∠CBP,进而得出结论.
解答 解:由折叠知,∠BPE=∠APB,AP=PE,
∵点P是AD中点,
∴AP=DP,
∴PD=PE,
∴∠PDE=∠PED,
∵2∠PDE+∠DPE=180°,2∠APB+∠DPE=180°,
∴∠PDE=∠APB,
∵AD∥BC,
∴∠APB=∠CBP,
∴∠PDE=∠PED=∠BPE=∠APB=∠CBP,
故选:D.
点评 本题属于折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.解决问题的关键是由等腰三角形的性质得出∠PDE=∠APB.

练习册系列答案
相关题目
2.某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,初四某班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是1,乙的成绩的方差是0.8.根据以上数据,下列说法正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.进入夏季后某款空调供不应求,厂家加班生产并销售,在第一个产销期的12天中,为提高产量,从第5天开始增加了工时生产成本,每台空调的成本P(元)与时间x(天)的关系如表:
已知每天生产的空调数量y(台)与时间x(天)近似满足函数关系y=2x+16,每台空调的出售价格为1400元.
请解答下列问题:
(1)设厂家的日销售利润为W元,求W(元)与时间x(天)的函数关系式;
(2)确定该厂哪一天获得最大利润,最大利润是多少?
(3)设厂家在第一个产销期,获得最大利润时的成本为P1,日生产量为y1.
现计划从第13天开始,按每台成本P1元,每台生产y1台进行生产并完全售出,但由于机器损耗等原因,实际平均每台空调的成本比统计增加了a%,使得厂家10天的销售利润与原计划的8天的销售利润持平,求a的值.
| 时间x(天) | 每台空调的成本P(元) |
| 0<x≤5 | P=400 |
| 5<x≤12 | P=40x+200 |
请解答下列问题:
(1)设厂家的日销售利润为W元,求W(元)与时间x(天)的函数关系式;
(2)确定该厂哪一天获得最大利润,最大利润是多少?
(3)设厂家在第一个产销期,获得最大利润时的成本为P1,日生产量为y1.
现计划从第13天开始,按每台成本P1元,每台生产y1台进行生产并完全售出,但由于机器损耗等原因,实际平均每台空调的成本比统计增加了a%,使得厂家10天的销售利润与原计划的8天的销售利润持平,求a的值.
4.若点(-2,y1)、(-1,y2)在反比例函数y=-$\frac{6}{x}$的图象上,则下列结论正确的是( )
| A. | y1>y2>0 | B. | y2>y1>0 | C. | 0>y1>y2 | D. | 0>y2>y1 |
1.已知$\left\{\begin{array}{l}{a+6b=8}\\{3a+4b=16}\end{array}\right.$,则a-b等于( )
| A. | 4 | B. | $\frac{16}{3}$ | C. | 6 | D. | 2 |
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
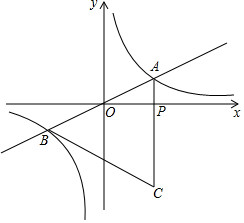 如图,直线y=kx与双曲线y=$\frac{\sqrt{3}}{x}$在一三象限分别交于A、B两点,等边△ABC的边AC交x轴于P点.
如图,直线y=kx与双曲线y=$\frac{\sqrt{3}}{x}$在一三象限分别交于A、B两点,等边△ABC的边AC交x轴于P点.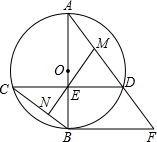 如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.
如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.