题目内容
蜡烛燃烧时,剩下的长度y(cm)是燃烧时间x(小时)的一次函数,现测得蜡烛燃烧1小时后其长度为15cm,燃烧2小时后其长度为10cm.
(1)写出y与x的函数关系式;
(2)蜡烛原长是多少?
(3)蜡烛燃烧完需多少小时?
(1)写出y与x的函数关系式;
(2)蜡烛原长是多少?
(3)蜡烛燃烧完需多少小时?
考点:一次函数的应用
专题:
分析:(1)由蜡烛燃烧时,剩下的长度y(cm)是燃烧时间x(小时)的一次函数,可设y=kx+b,将x=1,y=15;x=2,y=10代入,利用待定系数法即可求出y与x的函数关系式;
(2)将x=0代入(1)中所求的解析式,求出的y值即为蜡烛原长;
(3)将y=0代入(1)中所求的解析式,求出x即可.
(2)将x=0代入(1)中所求的解析式,求出的y值即为蜡烛原长;
(3)将y=0代入(1)中所求的解析式,求出x即可.
解答:解:(1)设y=kx+b,
将x=1,y=15;x=2,y=10代入,得
,解得
,
故y与x的函数关系式为y=-5x+20;
(2)∵y=-5x+20,
∴当x=0时,y=20,
即蜡烛原长是20cm;
(3)∵y=-5x+20,
∴当y=0时,-5x+20=0,
解得x=4,
即蜡烛燃烧完需4小时.
将x=1,y=15;x=2,y=10代入,得
|
|
故y与x的函数关系式为y=-5x+20;
(2)∵y=-5x+20,
∴当x=0时,y=20,
即蜡烛原长是20cm;
(3)∵y=-5x+20,
∴当y=0时,-5x+20=0,
解得x=4,
即蜡烛燃烧完需4小时.
点评:此题考查了一次函数的应用;利用待定系数法求出y与x之间的函数关系式是解题的关键.

练习册系列答案
相关题目
 如图,线段AB两个端点的坐标分别是A(6,4),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的
如图,线段AB两个端点的坐标分别是A(6,4),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的| 1 |
| 2 |
| A、(3,2) |
| B、(4,1) |
| C、(3,1) |
| D、(4,2) |
 如图,AC∥EF∥BD.求证:
如图,AC∥EF∥BD.求证: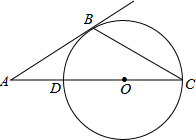 如图,AC经过圆心O交⊙O于点D,AB与⊙O相切于点B.若∠A=x(0°<x<90°)∠C=y,则y与x之间的函数关系图象是( )
如图,AC经过圆心O交⊙O于点D,AB与⊙O相切于点B.若∠A=x(0°<x<90°)∠C=y,则y与x之间的函数关系图象是( )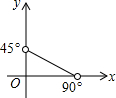
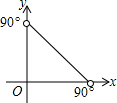


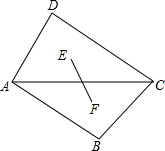 将两块三角尺按如图方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=12,点E,F分别是△ACD,△ABC的重心,求EF的长.
将两块三角尺按如图方式拼好,其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=12,点E,F分别是△ACD,△ABC的重心,求EF的长. 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推