题目内容

19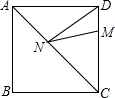．如图，已知正方形ABCD的边长为16，M在DC上，且DM=4，N是AC上的一动点，则DN+MN的最小值是20．

分析 连接BN，由轴对称图形的性质可知BN=DN，从而将DN+MN的最小值转化为BM的长求解即可．

解答 解：连接BN．

∵四边形ABCD是正方形，
∴NB=ND．
∴DN+MN=BN+MN．
当点B、N、M在同一条直线上时，ND+MN有最小值．
由勾股定理得：BM=$\sqrt{M{C}^{2}+B{C}^{2}}$=20．
故答案为：20．

点评 本题主要考查的是轴对称的性质、正方形的性质、勾股定理的应用，明确当点B、N、M在同一条直线上时，ND+MN有最小值时解题的关键．

练习册系列答案
相关题目
18．计算题
（1）4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
（2）（$\sqrt{2}+1）$（$\sqrt{2}-1）$+（$\sqrt{3}-2）^{2}$2．
10．对于平面直角坐标系 xOy中的点P（a，b），若点P′的坐标为（$a+\frac{b}{k}$，ka+b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”． 例如：P（1，4）的“2属派生点”为P′（1+$\frac{4}{2}$，2×1+4），即P′（3，6）．
（1）点P（-1，-2）的“2属派生点”P′的坐标为（-2，-4）；
（2）若点P在x轴的正半轴上，点P的“k属派生点”为P'点，且△OPP′为等腰直角三角形，求k的值；
（3）已知点Q为二次函数$y={x^2}+4\sqrt{3}x+16$图象上的一动点，点A在函数$y=-\frac{{4\sqrt{3}}}{x}$（x＜0）的图象上，且点A是点B的“$-\sqrt{3}$属派生点”，当线段B Q最短时，求Q点坐标．
7．若$\sqrt{{k}^{2}}$=-k，则k在数轴上原点的左侧（k≠0）．
14．请指出下列命题的题设和结论，并判断它们的真假，若是假命题，请举出一个反例．
（1）等角的补角相等；
（2）绝对值相等的两个数相等．
4．已知$\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$是方程组$\left\{{\begin{array}{l}{ax+by=5}\\{bx+ay=1}\end{array}}\right.$的解，则a-b的值是4．
11．探索：在图1至图3中，已知△ABC的面积为a，

（1）如图1，延长△ABC的边BC到点D，使CD=BC，连接DA．若△ACD的面积为S1，则S1=a（用含a的代数式表示）
（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连接DE．若△DEC的面积为S2，则S2=2a（用含a的代数式表示）
（3）在图2的基础上延长AB到点F，使BF=AB，连接FD，FE，得到△DEF（如图3）．若阴影部分的面积为S3，则S3=6a（用含a的代数式表示）．
发现：像上面那样，将△ABC各边均顺次延长一倍，连接所得端点，得到△DEF（如图3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的7倍．
应用：要在一块足够大的空地上栽种花卉，工程人员进行了如下的图案设计：首先在△ABC的空地上种红花，然后将△ABC向外扩展三次（图4已给出了前两次扩展的图案）．在第一次扩展区域内种黄花，第二次扩展区域内种紫花，第三次扩展区域内种蓝花．如果种红花的区域（即△ABC）的面积是10平方米，请你运用上述结论求出：
（1）种紫花的区域的面积；
（2）种蓝花的区域的面积．
8．已知：a-b=$\frac{1}{5}$，a2+b2=2$\frac{1}{25}$，求（ab）2016的值．
9．不等式1-2x≤5的解集在数轴上表示为（　　）
A．B．C．D．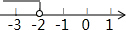

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网