题目内容
4.已知$\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$是方程组$\left\{{\begin{array}{l}{ax+by=5}\\{bx+ay=1}\end{array}}\right.$的解,则a-b的值是4.分析 把x与y的值代入方程组求出a与b的值,即可确定出a-b的值.
解答 解:把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}{2a+b=5①}\\{2b+a=1②}\end{array}\right.$,
①×2-②得:3a=9,即a=3,
把a=3代入②得:b=-1,
则a-b=3+1=4,
故答案为:4.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
9.下列等式正确的是( )
| A. | (-x2)3=-x5 | B. | x3+x3=2x6 | C. | a3•a3=2a3 | D. | 26+26=27 |
16.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{12}$÷$\sqrt{3}$=2 | C. | $\sqrt{6}$×(-$\sqrt{3}$)=3$\sqrt{2}$ | D. | ($\sqrt{3}$-1)2=2 |
13.在平面直角坐标系中,点P(2,-1)关于原点O的对称点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.下列各式中,有意义的是( )
| A. | $\sqrt{\frac{1}{9}-1}$ | B. | $\sqrt{-2}$ | C. | $-\sqrt{{{({-6})}^3}}$ | D. | $\sqrt{{{({-3})}^2}}$ |
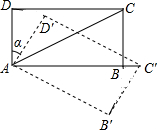 如图,在长方形ABCD中,AB=$\sqrt{3}$,AD=1,该长方形绕点A顺时针旋转α度得长方形AB′C′D′,点C′落在AB的延长线上,则线段BC′的长是2-$\sqrt{3}$.
如图,在长方形ABCD中,AB=$\sqrt{3}$,AD=1,该长方形绕点A顺时针旋转α度得长方形AB′C′D′,点C′落在AB的延长线上,则线段BC′的长是2-$\sqrt{3}$.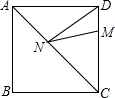 如图,已知正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是20.
如图,已知正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是20.