题目内容
 如图,△ABC的外角∠DAC的平分线与内角∠ABC的平分线交于点E.若∠C=60°,求∠E.
如图,△ABC的外角∠DAC的平分线与内角∠ABC的平分线交于点E.若∠C=60°,求∠E.考点:三角形内角和定理,三角形的外角性质
专题:
分析:先设∠ABC=x°,再用x表示出∠BAC的度数,根据角平分线的性质求出∠ABE及∠CAE的度数,由三角形内角和定理即可得出结论.
解答:解:设∠ABC=x°,则∠BAC=180°-∠ABC-∠C=180°-x°-60°=120°-x°,
∵△ABC的外角∠DAC的平分线与内角∠ABC的平分线交于点E,
∴∠ABE=
∠ABC=
x°,∠CAE=
(x°+60°)=
x°+30°,
∴∠E=180°-∠ABE-∠BAC-∠CAE=180°-
x°-(120°-x°)-
x°-30°=180°-
x°-120°+x°-
x°-30°=30°.
∵△ABC的外角∠DAC的平分线与内角∠ABC的平分线交于点E,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E=180°-∠ABE-∠BAC-∠CAE=180°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD中,∠B=90°,AB=BC=
如图,四边形ABCD中,∠B=90°,AB=BC=
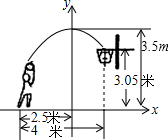 如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.
如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米. 如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是
如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是