题目内容
小明和同桌小聪在课后预习时,对课本中的一道思考题,进行了认真的探索:
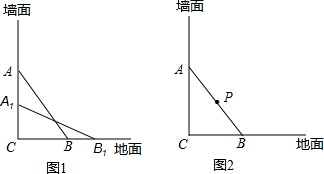
如图1,一架5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为3米.如果梯子的顶端沿墙下滑2米,那么点B将向外移动几米?
(1)请你将小明对“思考题”的解答补充完整:
解:在Rt△ABC中,由勾股定理得AB2=AC2+BC2,即52=AC2+32
∴AC= .
∵AA1=2,
∴A1C= .
在Rt△A1B1C中,由勾股定理得A1B12=A1C2+B1C2,
∴B1C= .
∴点B将向外移动 米.
(2)解完“思考题”后,小聪提出了如下两个问题,请你解答:
①如图1,在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
②若某人站在梯子的正中间P处(即梯子AB的中点),试问在梯子下滑过程中,请你在备用图中画出此人移动的路程(即点P移动的轨迹),并求出这个路程.

如图1,一架5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙底端C的距离为3米.如果梯子的顶端沿墙下滑2米,那么点B将向外移动几米?
(1)请你将小明对“思考题”的解答补充完整:
解:在Rt△ABC中,由勾股定理得AB2=AC2+BC2,即52=AC2+32
∴AC=
∵AA1=2,
∴A1C=
在Rt△A1B1C中,由勾股定理得A1B12=A1C2+B1C2,
∴B1C=
∴点B将向外移动
(2)解完“思考题”后,小聪提出了如下两个问题,请你解答:
①如图1,在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
②若某人站在梯子的正中间P处(即梯子AB的中点),试问在梯子下滑过程中,请你在备用图中画出此人移动的路程(即点P移动的轨迹),并求出这个路程.
考点:勾股定理的应用
专题:
分析:(1)直接把数值代入计算即可;
(2)①设梯子顶端从A处下滑x米,点B向外也移动x米,根据题意列出方程,解这个方程即可;
②此人移动的路程(即点P移动的轨迹)是半径为
,与墙面和地面相切的圆的
,所以结果为
π.
(2)①设梯子顶端从A处下滑x米,点B向外也移动x米,根据题意列出方程,解这个方程即可;
②此人移动的路程(即点P移动的轨迹)是半径为
| 5 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
解答:解:(1)由52=AC2+32
可知AC=
=4,
A1C=AC-AA1=4-2=2,
由勾股定理得A1B12=A1C2+B1C2,
∴B1C=
=
=
∴点B将向外移动BB1=
-3;
(2)①有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+3)2+(4-x)2=52,
解得:x1=1或x2=0(舍)
∴当梯子顶端从A处下滑1米时,点B向外也移动1米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.

②如图2,此人移动的路程(即点P移动的轨迹)是半径为
,与墙面和地面相切的圆的
,
即
π.
可知AC=
| 52-32 |
A1C=AC-AA1=4-2=2,
由勾股定理得A1B12=A1C2+B1C2,
∴B1C=
| A1B12-B 1C2 |
| 52-22 |
| 21 |
∴点B将向外移动BB1=
| 21 |
(2)①有可能.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+3)2+(4-x)2=52,
解得:x1=1或x2=0(舍)
∴当梯子顶端从A处下滑1米时,点B向外也移动1米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.

②如图2,此人移动的路程(即点P移动的轨迹)是半径为
| 5 |
| 2 |
| 1 |
| 4 |
即
| 5 |
| 4 |
点评:本题考查的是解直角三角形的应用及一元二次方程的应用,根据题意得出关于x的一元二次方程是解答此题的关键.

练习册系列答案
相关题目
菱形ABCD中,有一个角为120°,较长的对角线长为4
,则菱形的面积为( )
| 3 |
A、8
| ||
B、12
| ||
C、16
| ||
D、32
|
用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为( )
| A、a,b都能被3整除 |
| B、a不能被3整除 |
| C、a,b不都能被3整除 |
| D、a,b都不能被3整除 |
若x2+x=2,则代数式x3+3x2+2011的值是( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
 如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100
如图所示,在一次夏令营活动中,小明坐车从营地A点出发,沿北偏东60°方向走了100 将连续奇数1,3,5,7,9…排列成如图数表
将连续奇数1,3,5,7,9…排列成如图数表 尺规作图(保留作图痕迹,不写作法)如图,已知线段 a,h,求作以a为底、h为高的等腰三角形.
尺规作图(保留作图痕迹,不写作法)如图,已知线段 a,h,求作以a为底、h为高的等腰三角形.