题目内容
菱形ABCD中，有一个角为120°，较长的对角线长为4
，则菱形的面积为（ ）
| 3 |
A、8
| ||
B、12
| ||
C、16
| ||
D、32
|
考点：菱形的性质
专题：
分析：由菱形ABCD中，对角线AC和BD相交于点O，∠BAD=120°，BD=4
，可求得∠BAC的度数，利用菱形的性质可求出∠ABO的度数，进而得到AO的长，根据菱形的面积等于对角线乘积的一半则可求得答案．
| 3 |
解答：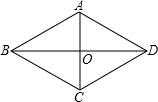
解：∵菱形ABCD中，∠BAD=120°，
∴∠BAC=
∠BAD=60°，AC⊥BD，
∴∠ABO=30°，
∵BD=4
，
∴BO=2
，
∴AO=2，
∴AC=4，
∴菱形的面积=4
×4÷2=8
，
故选A．
解：∵菱形ABCD中，∠BAD=120°，∴∠BAC=
| 1 |
| 2 |
∴∠ABO=30°，
∵BD=4
| 3 |
∴BO=2
| 3 |
∴AO=2，
∴AC=4，
∴菱形的面积=4
| 3 |
| 3 |
故选A．
点评：此题考查了菱形的性质、含30°角的直角三角形的性质以及勾股定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行．从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A55的坐标是在下列数：-|-3|，（-3）2，-（-3），-32中，负数的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
下列调查适合采用“普查”的是（ ）
| A、了解在校大学生的主要娱乐方式 |
| B、了解某个班级学生的体重 |
| C、一批灯泡的使用寿命 |
| D、调查《新闻联播》电视栏目的收视率 |
如图，线段AB=2cm，把线段AB向右平移3cm，得到线段DC，连接BC、AD，则四边形ABCD的面积为（ ）| A、4cm2 |
| B、9cm2 |
| C、6cm2 |
| D、无法确定 |
如图，点A、B、C、D、0都在方格纸的格点上，将△ABO绕点O按逆时针方向旋转得到△COD，则旋转的角度可以为（ ）| A、30° | B、45° |
| C、90° | D、135° |
