题目内容
10.已知a+b+c=0,则$\frac{a^2}{{2{a^2}+bc}}+\frac{b^2}{{2{b^2}+ac}}+\frac{c^2}{{2{c^2}+ab}}$值为1.分析 由a+b+c=0,得到c=-a-b,代入原式中计算即可得到结果.
解答 解:∵a+b+c=0,
∴c=-a-b,
∴原式=$\frac{{a}^{2}}{2{a}^{2}+b(-a-b)}$+$\frac{{b}^{2}}{2{b}^{2}+a(-a-b)}$+$\frac{{(-a-b)}^{2}}{2{(-a-b)}^{2}+ab}$
=$\frac{{a}^{2}}{2{a}^{2}-b(a+b)}$+$\frac{{b}^{2}}{2{b}^{2}-a(a+b)}$+$\frac{{(-a-b)}^{2}}{2{(a+b)}^{2}+ab}$
=$\frac{(a-b)(2ab+{a}^{2}+{b}^{2}+ab)}{(a-b)(2a+b)(2b+a)}$+$\frac{{a}^{2}+{b}^{2}+2ab}{2{a}^{2}+2+5ab}$
=$\frac{2ab+{a}^{2}+{b}^{2}+ab}{(2a+b)(2b+a)}$+$\frac{{a}^{2}+{b}^{2}+2ab}{(2a+b)(2b+a)}$
=$\frac{2{a}^{2}+2{b}^{2}+5ab}{2{a}^{2}+2{b}^{2}+5ab}$
=1.
故答案为:1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
18.下列长度的三条线段,能组成三角形的是( )
| A. | 4cm、5cm、9cm | B. | 8cm、7cm、15cm | C. | 5cm、5cm、11cm | D. | 13cm、12cm、20cm |
20.已知抛物线y=x2-2mx+m2+m+2与x轴的交点为(a,0),(b,0),则(a-1)2+(b-1)2的最小值是( )
| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
 如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线(保留作图痕迹,不要求写出作法).
如图,已知线段AB.用尺规作图的方法作出线段AB的垂直平分线(保留作图痕迹,不要求写出作法). 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=35°,求∠2的度数.
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=35°,求∠2的度数.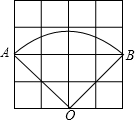 如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).
如图,在4×4的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.O、A、B分别是小正方形的顶点,求扇形OAB的弧长,周长和面积.(结果保留根号及π).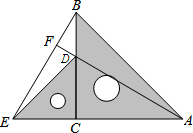 把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.
把两个含有45°角的直角三角板如图放置,点D在BC点上,连接BE、AD,AD的延长线交BE于点F,则∠AFB=90°.