题目内容
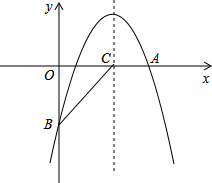 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 3 |
(1)求该抛物线的解析式;
(2)若抛物线对称轴与x轴交于点C,连接BC,点P在抛物线对称轴上,使△PBC为等腰三角形,请写出符合条件的所有点P坐标.(直接写出答案)
考点:抛物线与x轴的交点,待定系数法求二次函数解析式,等腰三角形的判定
专题:
分析:(1)把点A、B的坐标分别代入抛物线解析式,通过待定系数法来求b、c的值;
(1)需要分类讨论:BC=BP、BC=CP、BP=CP这三种情况下的点P的坐标.
(1)需要分类讨论:BC=BP、BC=CP、BP=CP这三种情况下的点P的坐标.
解答: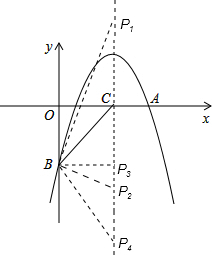 (1)∵抛物线经过点B(0,-4)
(1)∵抛物线经过点B(0,-4)
∴c=-4.
又抛物线y=-
x2+bx+c经过点A(6,0),
∴0=-
×62+6b-4
∴b=
∴该抛物线的解析式为:y=-
x2+
x-4;
(2)由(1)知,抛物线的解析式为:y=-
x2+
x-4.则对称轴为x=4,C(4,0).
∵B(0,-4),
∴BC=4
.
①当BC=CP时,CP=±4
,则P1(4,4
),P2(4,-4
);
②当BP=CP时,点P是线段BC的中垂线与直线x=4的交点,此时P3(4,-4);
③当BC=BP时,CP4=2CP3=8,此时P4(4,-8);
综上所述,符合题意的点P的坐标分别是:P1(4,4
),P2(4,-4
),P3(4,-4),P4(4,-8).
 (1)∵抛物线经过点B(0,-4)
(1)∵抛物线经过点B(0,-4)∴c=-4.
又抛物线y=-
| 1 |
| 3 |
∴0=-
| 1 |
| 3 |
∴b=
| 8 |
| 3 |
∴该抛物线的解析式为:y=-
| 1 |
| 3 |
| 8 |
| 3 |
(2)由(1)知,抛物线的解析式为:y=-
| 1 |
| 3 |
| 8 |
| 3 |
∵B(0,-4),
∴BC=4
| 2 |
①当BC=CP时,CP=±4
| 2 |
| 2 |
| 2 |
②当BP=CP时,点P是线段BC的中垂线与直线x=4的交点,此时P3(4,-4);
③当BC=BP时,CP4=2CP3=8,此时P4(4,-8);
综上所述,符合题意的点P的坐标分别是:P1(4,4
| 2 |
| 2 |
点评:本题考查抛物线与x轴的交点,等腰等腰三角形的性质.题目中没有指出等腰三角形的底边,所以解题时要分类讨论,以防漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
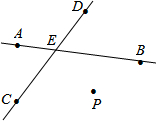 如图,直线CD与直线AB相交于E,根据下列语句画图.
如图,直线CD与直线AB相交于E,根据下列语句画图.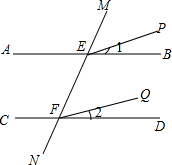 阅读理解并在括号内填注理由:
阅读理解并在括号内填注理由: