题目内容
 阅读理解并在括号内填注理由:
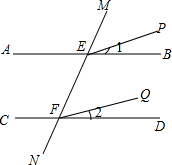
阅读理解并在括号内填注理由:如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
证明:∵AB∥CD,
∴∠MEB=∠MFD
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠
∴EP∥
考点:平行线的判定与性质
专题:推理填空题
分析:由AB与CD平行,利用两直线平行同位角相等得到一对角相等,再由已知角相等,利用等式的性质得到一对同位角相等,可得出EP与FQ平行.
解答:解:证明:∵AB∥CD,
∴∠MEB=∠MFD(两直线平行同位角相等),
又∵∠1=∠2(已知),
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠MFQ,
∴EP∥FQ(同位角相等两直线平行).
故答案为:两直线平行同位角相等;已知;MFQ;FQ;同位角相等两直线平行
∴∠MEB=∠MFD(两直线平行同位角相等),
又∵∠1=∠2(已知),
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠MFQ,
∴EP∥FQ(同位角相等两直线平行).
故答案为:两直线平行同位角相等;已知;MFQ;FQ;同位角相等两直线平行
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
相关题目
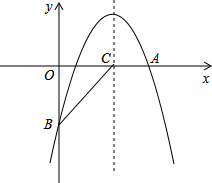 如图,抛物线
如图,抛物线
 一次函数y=kx+b的图象如图,当y<0时,x的取值范围是
一次函数y=kx+b的图象如图,当y<0时,x的取值范围是