题目内容
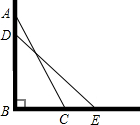 如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.
如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.(1)这个梯子的顶端A距离地面多远?
(2)如果梯子的顶端A下滑了4米,那么梯子底端C在水平方向滑动了4米吗?
考点:勾股定理的应用
专题:
分析:(1)在直角三角形ABC中,利用勾股定理即可求出AB的长即可;
(2)首先求出BD的长,利用勾股定理可求出BE的长,进而得到CE=BE-CB的值.
(2)首先求出BD的长,利用勾股定理可求出BE的长,进而得到CE=BE-CB的值.
解答:解:(1)在Rt△ABC中,由勾股定理得AB2+BC2=AC2,
即AB2+72=252,
所以AB=24(m),
即这架云梯的顶端A距地面有24m高;
(2)梯子的底端在水平方向滑动了8m.
理由:∵云梯的顶端A下滑了4m至点D,
∴BD=AB-AD=24-4=20(m),
在Rt△BDE中,由勾股定理得BD2+BE2=DE2,
即202+BE2=252
所以BE=15(m)
CE=BE-BC=15-7=8(m),
即梯子的底端在水平方向滑动了8m.
即AB2+72=252,
所以AB=24(m),

即这架云梯的顶端A距地面有24m高;
(2)梯子的底端在水平方向滑动了8m.
理由:∵云梯的顶端A下滑了4m至点D,
∴BD=AB-AD=24-4=20(m),
在Rt△BDE中,由勾股定理得BD2+BE2=DE2,
即202+BE2=252
所以BE=15(m)
CE=BE-BC=15-7=8(m),
即梯子的底端在水平方向滑动了8m.
点评:本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,将长方形纸条沿AB折叠,再将折起来的部分沿BC折叠至后面,已知∠1=20°,则∠2的度数等于( )
如图,将长方形纸条沿AB折叠,再将折起来的部分沿BC折叠至后面,已知∠1=20°,则∠2的度数等于( )| A、60° | B、70° |
| C、80° | D、90° |
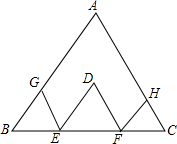 如图,D为△ABC内一点,过D作DE∥AB,DF∥AC,分别交BC于点E,F,过E作EG∥AC,交AB于点G,过F作FH∥AB,交AC于H.求证:BG+GE+ED+DF+FH+HC=AB+AC.
如图,D为△ABC内一点,过D作DE∥AB,DF∥AC,分别交BC于点E,F,过E作EG∥AC,交AB于点G,过F作FH∥AB,交AC于H.求证:BG+GE+ED+DF+FH+HC=AB+AC. 如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5.求BC的长.
如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5.求BC的长.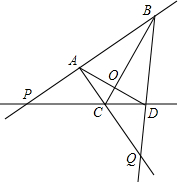 如图,已知A、B、C、D四个点.
如图,已知A、B、C、D四个点. 已知:如图,∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH.求证:GH∥MN.
已知:如图,∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH.求证:GH∥MN.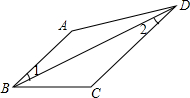 如图,在四边形ABCD中,∠A=130°,∠ADC=50°,试说明∠1=∠2.
如图,在四边形ABCD中,∠A=130°,∠ADC=50°,试说明∠1=∠2. 如图,已知AB∥CD,求证:∠BED=∠B+∠D.(提示:过点E作EF∥AB)
如图,已知AB∥CD,求证:∠BED=∠B+∠D.(提示:过点E作EF∥AB)