题目内容
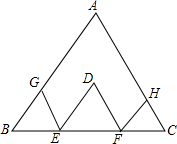 如图,D为△ABC内一点,过D作DE∥AB,DF∥AC,分别交BC于点E,F,过E作EG∥AC,交AB于点G,过F作FH∥AB,交AC于H.求证:BG+GE+ED+DF+FH+HC=AB+AC.
如图,D为△ABC内一点,过D作DE∥AB,DF∥AC,分别交BC于点E,F,过E作EG∥AC,交AB于点G,过F作FH∥AB,交AC于H.求证:BG+GE+ED+DF+FH+HC=AB+AC.考点:平行四边形的判定与性质
专题:证明题
分析:延长ED交AC于点I,延长FD交AB于点J,由条件可证明四边形AJFH和四边形DEGJ为平行四边形,可得到DE=GJ,HF=DI=AJ,可得到AB=BG+DE+HF,同理可得到AC=HC+DF+GE,可证得结论.
解答: 证明:如图,延长DE交AC于点I,延长FD交AB于点J,
证明:如图,延长DE交AC于点I,延长FD交AB于点J,
∵FH∥AB,DF∥AC,
∴四边形AJFH为平行四边形,
∴AJ=FH,
∵DF∥AC,GE∥AC,
∴GE∥DF,且DE∥AB,
∴四边形DEGJ为平行四边形,
∴GJ=DE,
∴AB=BG+GJ+AJ=BG+DE+HF,
同理可得AC=CH+DF+GE,
∴BG+GE+ED+DF+FH+HC=AB+AC.
 证明:如图,延长DE交AC于点I,延长FD交AB于点J,
证明:如图,延长DE交AC于点I,延长FD交AB于点J,∵FH∥AB,DF∥AC,
∴四边形AJFH为平行四边形,
∴AJ=FH,
∵DF∥AC,GE∥AC,
∴GE∥DF,且DE∥AB,
∴四边形DEGJ为平行四边形,
∴GJ=DE,
∴AB=BG+GJ+AJ=BG+DE+HF,
同理可得AC=CH+DF+GE,
∴BG+GE+ED+DF+FH+HC=AB+AC.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定方法是解题的关键.即①有两组对边分别平行的四边形是平行四边形,②有两组对边分别相等的四边形是平行四边形,③有一组对边平行且相等的四边形是平行四边形,④有两组对角分别相等的四边形是平行四边形,⑤对角线互相平分的四边形是平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两条直线被第三条直线所截,若有一对内错角相等,则这对内错角的角平分线( )
| A、互相垂直 |
| B、相交但不垂直 |
| C、互相平行 |
| D、位置关系无法确定 |
下列物体的主视图是圆的是( )
A、 圆柱 |
B、 圆锥 |
C、 球 |
D、 正方体 |
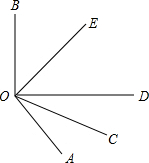 如图,OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°.
如图,OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130°.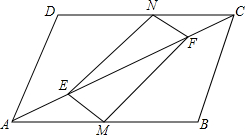 如图,在平行四边形ABCD中,M,N分别是AB,CD的中点,E,F是AC上两点,且AE=CF.
如图,在平行四边形ABCD中,M,N分别是AB,CD的中点,E,F是AC上两点,且AE=CF.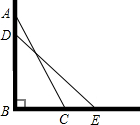 如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.
如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.