题目内容
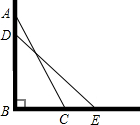
 如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5.求BC的长.
如图,点D是△ABC的BC边上的一点,已知AB=13,AD=12,AC=20,BD=5.求BC的长.考点:勾股定理的逆定理,勾股定理
专题:
分析:先根据勾股定理的逆定理判断出△ABD的形状,再根据勾股定理求出CD的长,进而可得出结论.
解答:解:∵AB=13,AD=12,BD=5,132=122+52,
∴△ABD是直角三角形.
∵AC=20,
∴CD=
=
=16,
∴BC=BD+CD=5+16=21.
∴△ABD是直角三角形.
∵AC=20,
∴CD=
| AC2-AD2 |
| 202-122 |
∴BC=BD+CD=5+16=21.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
两条直线被第三条直线所截,若有一对内错角相等,则这对内错角的角平分线( )
| A、互相垂直 |
| B、相交但不垂直 |
| C、互相平行 |
| D、位置关系无法确定 |
下列物体的主视图是圆的是( )
A、 圆柱 |
B、 圆锥 |
C、 球 |
D、 正方体 |
下列描述不正确的是( )
A、单项式-
| ||||
| B、用一个平面去截一个圆柱,截面的形状可能是一个长方形 | ||||
| C、过七边形的一个顶点有5条对角线 | ||||
| D、五棱柱有7个面,15条棱 |
设某数是x,若比它的2倍大3的数是8,可列方程为( )
| A、2x-3=8 | ||
| B、2x+3=8 | ||
C、
| ||
D、
|
已知点A(x,2)和点B(1,-2)关于原点对称,则x的值等于( )
| A、1 | B、-1 | C、-2 | D、2 |
 如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.
如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.