题目内容
 如图,已知AB∥CD,求证:∠BED=∠B+∠D.(提示:过点E作EF∥AB)
如图,已知AB∥CD,求证:∠BED=∠B+∠D.(提示:过点E作EF∥AB)考点:平行线的性质
专题:证明题
分析:过点E作EF∥AB,可得到EF∥CD,结合平行线的性质可证得结论.
解答:证明:
过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
下列物体的主视图是圆的是( )
A、 圆柱 |
B、 圆锥 |
C、 球 |
D、 正方体 |
下面的式子成立的是 ( )
| A、7ab-7ba=0 |
| B、5y2-2y2=3 |
| C、4x2y-5y2x=-x2y |
| D、a+a=2a2 |
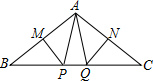 如图,△ABC中,MP和NQ分别垂直平分AB和AC,若∠PAQ=40°,则∠BAC的度数是( )
如图,△ABC中,MP和NQ分别垂直平分AB和AC,若∠PAQ=40°,则∠BAC的度数是( )| A、140° | B、110° |
| C、100° | D、70° |
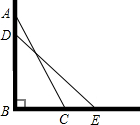 如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.
如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.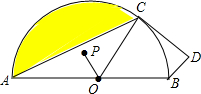 如图,AB是半⊙O的直径,CD切半⊙O于点C,P是△OAC的重心,且OP=
如图,AB是半⊙O的直径,CD切半⊙O于点C,P是△OAC的重心,且OP= 如图是一个圆柱形杯子的底面直径为6cm,高为8cm,则杯子内能容下的最长的木棒长为
如图是一个圆柱形杯子的底面直径为6cm,高为8cm,则杯子内能容下的最长的木棒长为 如图,△ABC的边长不变,BC边上的高AH的长为x在变化,若BC的长为8,则△ABC的面积y与x之间的函数关系式为
如图,△ABC的边长不变,BC边上的高AH的长为x在变化,若BC的长为8,则△ABC的面积y与x之间的函数关系式为