题目内容
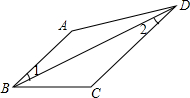 如图,在四边形ABCD中,∠A=130°,∠ADC=50°,试说明∠1=∠2.
如图,在四边形ABCD中,∠A=130°,∠ADC=50°,试说明∠1=∠2.请你完成下列填空,把解答过程补充完整.
证明:∵∠A=130°,∠ADC=50°(已知)
∴∠A+∠ADC=180°(等式的性质)
∴
∴∠1=∠2 (
考点:平行线的判定与性质
专题:推理填空题
分析:由条件可判定AB∥CD,再根据平行线的性质可得到∠1=∠2,据此填空即可.
解答:证明:∵∠A=130°,∠ADC=50°(已知)
∴∠A+∠ADC=180°(等式的性质)
∴AB∥CD ( 同旁内角互补,两直线平行)
∴∠1=∠2 ( 两直线平行,内错角相等)
故答案为:AB;CD;同旁内角互补,两直线平行;两直线平行,内错角相等.
∴∠A+∠ADC=180°(等式的性质)
∴AB∥CD ( 同旁内角互补,两直线平行)
∴∠1=∠2 ( 两直线平行,内错角相等)
故答案为:AB;CD;同旁内角互补,两直线平行;两直线平行,内错角相等.
点评:本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设某数是x,若比它的2倍大3的数是8,可列方程为( )
| A、2x-3=8 | ||
| B、2x+3=8 | ||
C、
| ||
D、
|
下面的式子成立的是 ( )
| A、7ab-7ba=0 |
| B、5y2-2y2=3 |
| C、4x2y-5y2x=-x2y |
| D、a+a=2a2 |
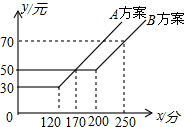 某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题:
某电信公司提供了A,B两种通讯方案,其通讯费用y(元)与通话时间x(分)之间的关系如图所示,观察图象,回答下列问题: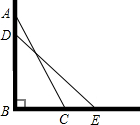 如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.
如图,一架25米长的云梯AC斜靠一面竖直的墙AB上,这时梯子底端C离墙7米.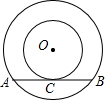 半径为5的大⊙O的弦与小⊙O相切于点C,且AB=8,则小⊙O的半径为
半径为5的大⊙O的弦与小⊙O相切于点C,且AB=8,则小⊙O的半径为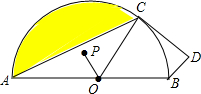 如图,AB是半⊙O的直径,CD切半⊙O于点C,P是△OAC的重心,且OP=
如图,AB是半⊙O的直径,CD切半⊙O于点C,P是△OAC的重心,且OP=