题目内容
1.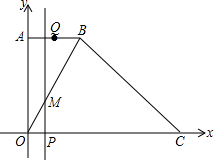 如图,在平面直角坐标系中,已知A(0,4),B(2,4),点C在x轴的正半轴上,且∠BCO=45°,连接OB.动点Q以每秒1个单位长度的速度,从点B沿折线B-A-O向点O运动.同时动点P以相同的速度,从点O沿线段OC向点C运动.过点P作直线PM⊥OC,与折线O-B-C相交于点M.当其中一点到达终点时,另一点也随之停止运动.设点P运动时间为t(秒).
如图,在平面直角坐标系中,已知A(0,4),B(2,4),点C在x轴的正半轴上,且∠BCO=45°,连接OB.动点Q以每秒1个单位长度的速度,从点B沿折线B-A-O向点O运动.同时动点P以相同的速度,从点O沿线段OC向点C运动.过点P作直线PM⊥OC,与折线O-B-C相交于点M.当其中一点到达终点时,另一点也随之停止运动.设点P运动时间为t(秒).(1)求C点坐标;
(2)当点Q在AB上时,连接QM、CM.问:△BQM能否与△OCM相似?若能,请求出P点坐标;若不能,请说明理由.
(3)当点Q在OA上时,探究:四边形OPMQ的周长是否发生变化?若不变,求出其周长;若变化,请说明理由.
分析 (1)过点B作BD⊥OC于D,构造直角三角形,求出点的坐标;
(2)由PM∥BD,得到△OPM∽△ODB,得到线段OP,PM的关系,当△BQM∽△OMC时,对应边成比例,列方程求得t的值;
(3)当点Q在OA上时,PM交BC于M,证出四边形OPMQ是矩形,求得矩形OPMQ的周长=2(6-t)+t+t=12是个定值,得到结论.
解答  解:(1)如图1过点B作BD⊥OC于D,
解:(1)如图1过点B作BD⊥OC于D,
∵B(2,4),
∴OD=2,BD=4,
∵∠BCO=45°,
∴CD=BD=4,
∴OC=6,
∴(6,0);
(2)能,
如图2∵PM∥BD,
∴△OPM∽△ODB,
∴$\frac{OP}{PM}$=$\frac{OD}{BD}$=$\frac{1}{2}$,
∵OB=$\sqrt{{BD}^{2}{+OD}^{2}}$=2$\sqrt{5}$,
当点Q在AB上时,
∵BQ=t,OP=t,
∴PM=2t,OM=$\sqrt{5}$t,BM=2$\sqrt{5}$-$\sqrt{5}$t,
当△BQM∽△OMC时,
$\frac{BQ}{OM}$=$\frac{BM}{OC}$,∴$\frac{t}{\sqrt{5}t}$=$\frac{2\sqrt{5}-\sqrt{5}t}{6}$,
∴t=$\frac{4}{5,}$,
∴当t=$\frac{4}{5}$时,△BQM∽△OCM;
(3)如图3当点Q在OA上时,PM交BC于M,
∵PM∥OA,OP=t,PC=6-t,
∵∠BCO=45°,
∴PM=6-t,OQ=4-(t-2)=6-t,
∴PM=OQ,
∴四边形OPMQ是矩形,
∴QM=OP=t,
∴矩形OPMQ的周长=2(6-t)+t+t=12是个定值,
∴当点Q在OA上时,四边形OPMQ的周长不会发生变化.
点评 本题考查了在平面直角坐标系中求点的坐标,相似三角形的判定和性质,动点问题,矩形的判定以及矩形的周长的求法,根据题意画出图形是解题的关键.


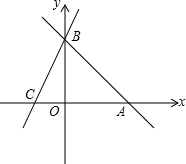 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.