题目内容
14. 如图,是一副形似“秋蝉”的图案,其实线部分是由正方形、正五边形和正六边形叠放在一起形成的,则图中∠MON的度数为33°.
如图,是一副形似“秋蝉”的图案,其实线部分是由正方形、正五边形和正六边形叠放在一起形成的,则图中∠MON的度数为33°.
分析 由正方形、正五边形和正六边形的性质得到∠AOM=108°,∠OBC=120°,∠NBC=90°,求得∠AOB=$\frac{1}{2}×$120°=60°,∠MOB=108°-60°=48°,得到∠OBN=360°-120°-90°=150°,根据角和差即可得到结论.
解答  解:由正方形、正五边形和正六边形的性质得,∠AOM=108°,∠OBC=120°,∠NBC=90°,
解:由正方形、正五边形和正六边形的性质得,∠AOM=108°,∠OBC=120°,∠NBC=90°,
∴∠AOB=$\frac{1}{2}×$120°=60°,∠MOB=108°-60°=48°,
∴∠OBN=360°-120°-90°=150°,
∴∠NOB=$\frac{1}{2}$(180°-150°)=15°,
∴∠MON=33°,
故答案为:33°.
点评 本题考查了多边形的内角和外角,熟练掌握正方形、正五边形和正六边形的内角的度数是解题的关键.

练习册系列答案
相关题目
4.2015年日照市人民政府投入1000万元用于改造乡村小学班班通工程建设,计划到2017年再追加投资210万元,如果每年的平均增长率相同,那么我市这两年该项投入的平均增长率为( )
| A. | 1.21% | B. | 8% | C. | 10% | D. | 12.1% |
5.位于武侯区“中国女鞋之都”的某制鞋企业为了了解初中学生穿鞋的尺码情况,选择对某校的40名女生进行了调查,结果如下表所示,那么在平均数、中位数、众数三个统计量中,该制鞋企业最感兴趣的统计量是众数,该统计量的数值是36码.
| 尺码(单位:码) | 33 | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 8 | 8 | 14 | 6 | 2 |
2.已知圆锥侧面展开图的面积为65πcm2,其底面圆半径为5cm,则圆锥的母线长是( )
| A. | 13cm | B. | 12cm | C. | 10cm | D. | 5cm |
9.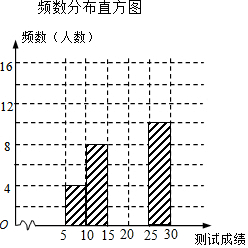 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
频数分布表
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于15分为合格,请你估计该校七年级学生有理数混合运算能力测试合格的人数?
 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 5≤x<10 | 4 |
| 第2组 | 10≤x<15 | 8 |
| 第3组 | 15≤x<20 | 16 |
| 第4组 | 20≤x<25 | a |
| 第5组 | 25≤x<30 | b |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于15分为合格,请你估计该校七年级学生有理数混合运算能力测试合格的人数?
 如图,已知一次函数y=-2x+b的图象与x轴、y轴分别交于B,A两点,与反比例函数y=$\frac{4}{x}$(x>0)交于C,D两点.
如图,已知一次函数y=-2x+b的图象与x轴、y轴分别交于B,A两点,与反比例函数y=$\frac{4}{x}$(x>0)交于C,D两点.



 一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )
一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )