题目内容
7.如图①,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式.
(3)若边EF与边AC交于点Q,连结PQ,如图②.
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出PQ的垂直平分线经过△ABC的顶点时t的值.
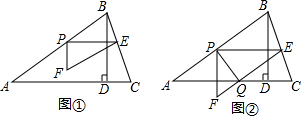
分析 (1)在Rt△ABD中,利用勾股定理求出AD,在Rt△BDC中,求出CD即可.
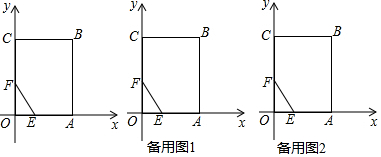
(2)①分两种情形求解:如图1中,当0<t≤1时,重叠部分是四边形PMDN.如图2中,当$\frac{25}{9}$≤t<5时,重叠部分是四边形PNMF.
②如图5中,当PQ的垂直平分线经过当A时.根据PE=PA,可得t=5-t解决问题.如图6中,当PQ的垂直平分线经过点B时,作EN⊥AC于N,EP交BD于M.在Rt△BQD中,根据BQ2=QD2+BD2,列出方程即可解决问题.
解答 解:(1)在Rt△ABD中,∠BDA=90°,AB=5,BD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,
∴CD=$\frac{BD}{tanC}$=$\frac{3}{3}$=1,
∴AC=AD+CD=4+1=5.
(2)如图1中,当0<t≤1时,重叠部分是四边形PMDN.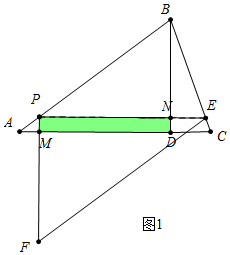
易知PA=t,AM=$\frac{4}{5}$t,PM=$\frac{3}{5}$t,DM=4-$\frac{4}{5}$t,
∴S=$\frac{3}{5}$t•(4-$\frac{4}{5}$t)=-$\frac{12}{25}$t2+$\frac{12}{5}$t.
如图2中,当$\frac{25}{9}$≤t<5时,重叠部分是四边形PNMF.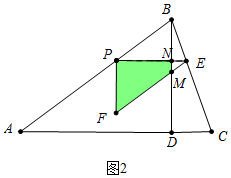
∵AB=5,AC=AD+CD=4+1=5,
∴AC=AB,
易证PB=PE=5-t,PF=$\frac{3}{4}$(5-t),PN=$\frac{4}{5}$(5-t),
S=$\frac{1}{2}$(5-t)•$\frac{3}{4}$(5-t)-$\frac{1}{2}$•$\frac{1}{5}$(5-t)•$\frac{3}{4}$•$\frac{1}{5}$(5-t)=$\frac{9}{25}$(5-t)2.
(3)①如图3中,PF交AC于G.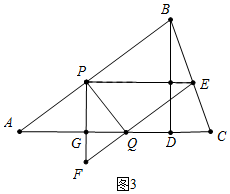
当S△PFQ:S△PEQ=1:2时,
∴S△PEQ:S△PEF=2:3,
∴$\frac{1}{2}$•PE•PG:$\frac{1}{2}$•PE•PF=2:3,
∴PG:PF=2:3,
∴$\frac{3}{5}$t:$\frac{3}{4}$(5-t)=2:3.
∴t=$\frac{25}{11}$,即AP=$\frac{25}{11}$.
如图4中,当S△PFQ:S△PEQ=2:1时,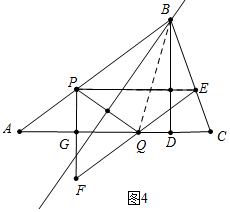
∴S△PEQ:S△PEF=1:3,
∴$\frac{1}{2}$•PE•PG:$\frac{1}{2}$•PE•PF=1:3,
∴PG:PF=1:3,
∴$\frac{3}{5}$t:$\frac{3}{4}$(5-t)=1:3.
∴t=$\frac{25}{17}$,即AP=$\frac{25}{17}$,
∴AP的值为$\frac{25}{11}$或$\frac{25}{17}$.
②如图5中,当PQ的垂直平分线经过当A时.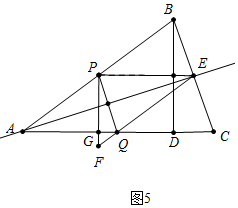
易知四边形APEQ时菱形,
∴PE=PA,即t=5-t,
∴t=$\frac{5}{2}$.
如图6中,当PQ的垂直平分线经过点B时,作EN⊥AC于N,EP交BD于M.
易知四边形PENG时矩形,四边形DMEN时矩形,
∴PG=EN=$\frac{3}{5}$t,EM=DN=PE-PM=$\frac{1}{5}$(5-t),
QN=$\frac{4}{3}$EN=$\frac{4}{5}$t,
∴QD=$\frac{4}{5}$t-$\frac{1}{5}$(5-t)=t-1,
在Rt△BQD中,∵BQ2=QD2+BD2,
∴(5-t)2=32+(t-1)2,
∴t=$\frac{15}{8}$.
综上所述,t=$\frac{15}{8}$s或$\frac{5}{2}$s时,△ABC的顶点.
点评 本题考查三角形综合题、解直角三角形、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考压轴题.

 小学教材完全解读系列答案
小学教材完全解读系列答案
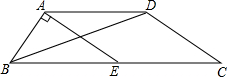 如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,点E是BC的中点,连接AE,BD,若EA⊥AB,BC=26,DC=12,求△ABD的面积.
如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,点E是BC的中点,连接AE,BD,若EA⊥AB,BC=26,DC=12,求△ABD的面积.