题目内容
13.不等式$\frac{x}{3}$>1-(x-3)的解集是x>3;不等式$\frac{x}{3}$>1-$\frac{x-3}{2}$的解集是x>3;
不等式$\frac{x}{3}$>1-$\frac{x-3}{3}$的解集是x>3;
…
不等式$\frac{x}{3}$>1-$\frac{x-3}{20}$的解集是x>3;
…
如果n是正数,则不等式$\frac{x}{3}$>1-$\frac{x-3}{n}$的解集是x>3.
当n是正数,且x>3时,请你用文字说明$\frac{x}{3}$>1-$\frac{x-3}{n}$的正确性.
分析 根据解不等式的步骤分别解每个不等式求出其解集,由n是正数且x>3可得$\frac{x}{3}$>1>1-$\frac{x-3}{n}$即可.
解答 解:解不等式$\frac{x}{3}$>1-(x-3),
去分母,得:x>3-3(x-3),
去括号,得:x>3-3x+9,
移项、合并,得:4x>12,
系数化为1,得:x>3;
解不等式$\frac{x}{3}$>1-$\frac{x-3}{2}$,
去分母,得:2x>6-3(x-3),
去括号,得:2x>6-3x+9,
移项、合并,得:5x>15,
系数化为1,得:x>3;
解不等式$\frac{x}{3}$>1-$\frac{x-3}{3}$
去分母,得:x>3-(x-3),
去括号,得:x>3-x+3,
移项、合并,得:2x>6,
系数化为1,得:x>3;
解不等式$\frac{x}{3}$>1-$\frac{x-3}{20}$,
去分母,得:20x>60-3(x-3),
去括号,得:20x>60-3x+9,
移项、合并,得:23x>69,
系数化为1,得:x>3;
解不等式$\frac{x}{3}$>1-$\frac{x-3}{n}$,
∵n>0,
∴去分母,得:nx>3n-3(x-3),
去括号,得:nx>3n-3x+9,
移项、合并,得:(n+3)x>3(n+3),
系数化为1,得:x>3;
当n>0,x>3时,$\frac{x}{3}$>1,$\frac{x-3}{n}$>0,
则$\frac{x}{3}$>1>1-$\frac{x-3}{n}$,
即$\frac{x}{3}$>1-$\frac{x-3}{n}$.
故答案为:x>3、x>3、x>3、x>3、x>3.
点评 本题主要考查解一元一次不等式的基本技能和不等式的基本性质的运用,熟练而准确解每个不等式是基础,根据n>0、x>3灵活应用不等式的基本性质判断$\frac{x}{3}$>1>1-$\frac{x-3}{n}$是关键.

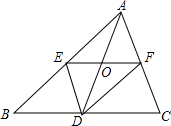 如图,在△ABC中,EF为△ABC的中位线,D为BC边上的中点,AD与EF交于点O,连结EF、DF.求证:四边形AEDF为平行四边形.
如图,在△ABC中,EF为△ABC的中位线,D为BC边上的中点,AD与EF交于点O,连结EF、DF.求证:四边形AEDF为平行四边形.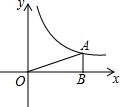 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(4,b).过点A作AB⊥x轴于点B,△AOB的面积为2.求:
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(4,b).过点A作AB⊥x轴于点B,△AOB的面积为2.求: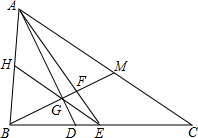 如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H.
如图,在△ABC中,AC>AB,AD是角平分线,AE是中线,BF⊥AD于点G,交AE于点F,交AC于点M,EG的延长线交AB于点H.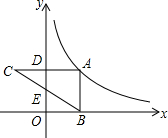 如图,点A在反比例函数y=$\frac{k}{2x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为12.
如图,点A在反比例函数y=$\frac{k}{2x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为12.