题目内容
12.函数y=-$\frac{1}{2x}$与y=-2x的图象的交点的坐标是($\frac{1}{2}$,-1),(-$\frac{1}{2}$,1).分析 把一次函数和反比例函数联立方程组求解即可.
解答 解:解$\left\{\begin{array}{l}{y=-\frac{1}{2x}}\\{y=-2x}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=1}\end{array}\right.$,
则函数y=-$\frac{1}{2x}$与y=-2x的图象的交点的坐标是($\frac{1}{2}$,-1),(-$\frac{1}{2}$,1).
故答案为:($\frac{1}{2}$,-1),(-$\frac{1}{2}$,1).
点评 本题考查了一次函数与反比例函数的交点问题,熟记解方程组的方法是解题的关键.

练习册系列答案
相关题目
20.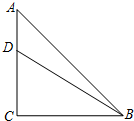 如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 4 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
17. 如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
 如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )| A. | 100m | B. | 100$\sqrt{3}$m | C. | 50$\sqrt{3}$m | D. | $50({\sqrt{3}+1})$m |
2.若x+y=9,x-y=1,则代数式2134-3(x2+y2)的值是( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
 如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2.
如图,△ABC在平面直角坐标系中第二象限内,顶点A的坐标是(-2,3),先把△ABC向右平移4个单位得到△A1B1C1,再作△A1B1C1关于x轴对称图形△A2B2C2. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,使点C与点A重合,点D落在点G处,求线段BF的长.
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,使点C与点A重合,点D落在点G处,求线段BF的长.