题目内容

1．如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，使点C与点A重合，点D落在点G处，求线段BF的长．

分析 根据将纸片ABCD沿直线EF折叠，使点C与点A重合得到AF=FC，根据勾股定理求出BF的长．

解答 解：∵A与C点关于EF成轴对称
∴AF=FC，
设BF=x，则AF=FC=8-x，
在Rt△ABF中，AB2+BF2=AF2，
即42+x2=（8-x）2，
解得x=3．
答：线段BF的长为3．

点评 本题考查的是翻折变换的性质和勾股定理的应用，掌握翻折变换的性质、找出对应线段是解题的关键．

练习册系列答案
相关题目
11．下列各式中，（1）$\frac{x+y}{x-y}$（2）$\frac{3}{{x}^{2}+1}$（3）$\frac{x}{3}$-$\frac{1}{x}$（4）$\frac{{x}^{2}+xy+{y}^{2}}{π}$（5）$\frac{a-b}{π-3.14}$（6）0．
整式是（4）、（5）、（6），分式是（1）、（2）、（3）．
12．函数y=-$\frac{1}{2x}$与y=-2x的图象的交点的坐标是（$\frac{1}{2}$，-1），（-$\frac{1}{2}$，1）．
9．已知二元一次方程2x-3y=1中，若x=3时，y=$\frac{5}{3}$；若y=1时，则x=2．
16．一列数按规律排列1，-2，$\frac{1}{3}$，-4，$\frac{3}{5}$，-6，…，则第99个数是$\frac{97}{99}$．
6．设⊙O的半径为r，圆心O到直线L的距离为d，若直线L与⊙O有交点，则d与r的关系为（　　）
A．d=rB．d＜rC．d＞rD．d≤r
13．下列说法中正确的是（　　）
A．两条对角线相等的四边形是矩形
B．两条对角线互相垂直的四边形是菱形
C．两条对角线互相垂直且相等的四边形是正方形
D．两条对角线互相平分的四边形是平行四边形
10．已知正方形ABCD中，对角线AC、BD相交于O．
①如图1，若E是AC上的点，过A 作AG⊥BE于G，AG、BD交于F，求证：OE=OF
②如图2，若点E在AC的延长线上，AG⊥EB交EB的延长线于G，AG延长DB延长线于点F，其它条件不变，OE=OF还成立吗？
11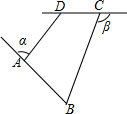．如图，已知四边形ABCD，∠α，∠β分别是∠BAD，∠BCD相邻的补角，且∠B+∠ADC=140°，则∠α+∠β等于（　　）
A．140°B．170°C．260°D．120°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网