题目内容
18. 若以△ABC的两边AB、BC为边分别向外作等腰直角△ABE和等腰直角BCH,连接AH、CE交于O点,取EH的中点N,连NB交AC于M.求证:
若以△ABC的两边AB、BC为边分别向外作等腰直角△ABE和等腰直角BCH,连接AH、CE交于O点,取EH的中点N,连NB交AC于M.求证:(1)AH=CE;
(2)AH⊥CE;
(3)NM⊥AC.
分析 (1)根据等腰直角三角形的性质得到AB=BE,BC=BH,∠ABE=∠CBH=90°,求得∠ABH=∠EBC,推出△ABH≌△EBC,根据全等三角形的性质得到结论;
(2)根据全等三角形的性质得到∠BAH=∠CEB,推出A,G,B,E四点共圆,根据圆周角定理得到∠AGE=∠ABE=90°,即可得到结论;
(3)延长BN到F使FN=BN,根据已知条件得到△BEN≌△HFN,根据全等三角形的性质得到HF=BE,∠1=∠F,推出∠ABC=∠BHF,通过△ABC≌△BHF,得到∠BAC=∠F,等量代换即可得到即可.
解答 证明:(1)∵△ABE与△BCH是等腰直角三角形,
∴AB=BE,BC=BH,∠ABE=∠CBH=90°,
∴∠ABH=∠EBC,
在△ABH与△EBC中,$\left\{\begin{array}{l}{AB=BE}\\{∠ABH=∠EBC}\\{BH=BC}\end{array}\right.$,
∴△ABH≌△EBC,
∴AH=CE;
(2)∵△ABH≌△EBC,
∴∠BAH=∠CEB,
∴A,G,B,E四点共圆,
∴∠AGE=∠ABE=90°,
∴AH⊥CE;
(3)延长BN到F使FN=BN,
在△BEN与△HFN中,$\left\{\begin{array}{l}{EN=HN}\\{∠ENB=∠HNF}\\{BN=FN}\end{array}\right.$,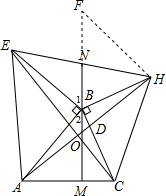
∴△BEN≌△HFN,
∴HF=BE,∠1=∠F,
∵∠ABC=180°-∠EBH=180°-∠1-∠HBN,
∠FHB=180°-∠F-∠FBH,
∴∠ABC=∠BHF,
∵AB=BE,
∴AB=HF,在△ABC与△BHF中,$\left\{\begin{array}{l}{AB=HF}\\{∠ABC=∠BHF}\\{BC=BH}\end{array}\right.$,
∴△ABC≌△BHF,
∴∠BAC=∠F,
∵∠1+∠2=90°,
∴∠BAM+∠2=90°,
∴∠AMB=90°,
∴NM⊥AC.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,熟练掌握全等三角形的判定和性质是解题的关键.

 如图为等边三角形ABC与正方形DEFG的重叠情形,其中D,E两点分别在AB,BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )
如图为等边三角形ABC与正方形DEFG的重叠情形,其中D,E两点分别在AB,BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )| A. | 6$\sqrt{2}$-6 | B. | 6$\sqrt{3}$-6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{3}$ |
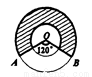
 π C. 2π D. 4π
π C. 2π D. 4π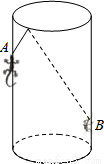
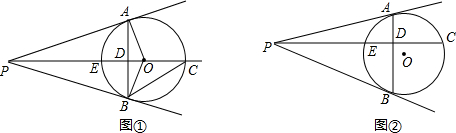
 如图,在△ABC中,AD是BC边上的中线,试说明点B和点C到AD所在的直线的距离相等(提示:根据点到直线的距离的定义作出相关的线段,再推理说明相关的线段相等)
如图,在△ABC中,AD是BC边上的中线,试说明点B和点C到AD所在的直线的距离相等(提示:根据点到直线的距离的定义作出相关的线段,再推理说明相关的线段相等) 如图,C是线段BE上一点,AC=BC=AB,CE=CD=DE,且△ACE和△BCD全等.
如图,C是线段BE上一点,AC=BC=AB,CE=CD=DE,且△ACE和△BCD全等.