题目内容
13. 如图,在△ABC中,AD是BC边上的中线,试说明点B和点C到AD所在的直线的距离相等(提示:根据点到直线的距离的定义作出相关的线段,再推理说明相关的线段相等)
如图,在△ABC中,AD是BC边上的中线,试说明点B和点C到AD所在的直线的距离相等(提示:根据点到直线的距离的定义作出相关的线段,再推理说明相关的线段相等)
分析 作BM⊥AD于M,CN⊥AD与N,∠M=∠CND=90°,由中线的定义得出BD=CD,由AAS证明△BDM≌△CDN,得出对应边相等BM=CN,即可得出结论.
解答 证明:作BM⊥AD于M,CN⊥AD与N,如图所示: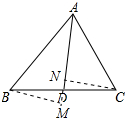
则∠M=∠CND=90°,
∵AD是BC边上的中线,
∴BD=CD,
在△BDM和△CDN中,$\left\{\begin{array}{l}{∠M=∠CND}&{\;}\\{∠BDM=∠CDN}&{\;}\\{BD=CD}&{\;}\end{array}\right.$,
∴△BDM≌△CDN(AAS),
∴BM=CN,
即点B和点C到AD所在的直线的距离相等.
点评 本题考查了全等三角形的判定与性质、三角形的中线等知识;证明三角形全等是解决问题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
3.两个不相等的正数a,b满足关系a+b=1,ab=t-1,设S=a3+b3,则s关于t的函数图象是( )
| A. | 射线(不含端点) | B. | 线段(不含端点) | C. | 直线 | D. | 抛物线的一部分 |
 ;④
;④ .其中结论正确的个数是( ).
.其中结论正确的个数是( ).
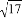 ;
;
 若以△ABC的两边AB、BC为边分别向外作等腰直角△ABE和等腰直角BCH,连接AH、CE交于O点,取EH的中点N,连NB交AC于M.求证:
若以△ABC的两边AB、BC为边分别向外作等腰直角△ABE和等腰直角BCH,连接AH、CE交于O点,取EH的中点N,连NB交AC于M.求证: 如图,AD=CF,BC=ED,BC∥ED,试判断AB与EF之间的关系,并说明理由.
如图,AD=CF,BC=ED,BC∥ED,试判断AB与EF之间的关系,并说明理由.