题目内容
12.如图,△ABC内接于⊙O,AB=AC,D在劣弧AC上,∠ABD=45°.(1)如图1,BD交AC于E,连CD,若AB=BD,求证:CD=$\sqrt{2}$DE;
(2)如图2,连AD、CD,已知tan∠CAD=$\frac{1}{5}$,求sin∠BDC.
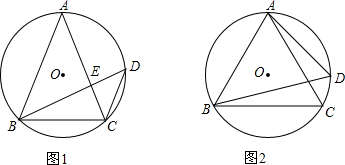
分析 (1)根据AB=AC,AB=BD得AC=BD,利用圆周角定理,得弧相等,∠ACD=∠ABD=45°,△EDC为等腰直角三角形,得证;
(2)作辅助线,构建直角三角形,利用边角关系与已知条件,得出结论.
解答 (1)证明:∵AB=AC,AB=BD,
∴AC=BD,
∴$\widehat{AC}=\widehat{BD}$,
∴$\widehat{BC}=\widehat{AD}$,
∴∠BDC=∠ABD=45°,
∵∠ACD=∠ABD=45°,
∴△EDC为等腰直角三角形,
∴CD=$\sqrt{2}$DE;
(2)解:做DG⊥AC于G,作ON⊥AC于N,延长AO交BC于M,
tan∠CAD=$\frac{DG}{AG}=\frac{1}{5}$,
令DG=GC=1,AG=5,
∴AC=6,AD=$\sqrt{26}$,
∴$OA=\frac{\sqrt{2}}{2}AD$=$\sqrt{13}$,OC=$\sqrt{13}$,
∵ON⊥AC,
∴$AN=\frac{1}{2}AC=3$,
∵$\frac{AN}{AM}=\frac{OA}{AC}$,
∴$AM=\frac{18}{13}\sqrt{13}$,
∵OM=AM-OA=$\frac{5}{13}\sqrt{13}$,MC=$\frac{12}{13}\sqrt{13}$,
∴sin∠BDC=sin∠MOC=$\frac{MC}{OC}$=$\frac{12}{13}$.
点评 本题主要考查了圆周角定理和解直角三角形,熟练运用圆周角定理,构建直角三角形是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
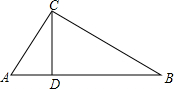 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=32°,CD=6,求AB的长.(结果保留到0.1)(已知sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=32°,CD=6,求AB的长.(结果保留到0.1)(已知sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)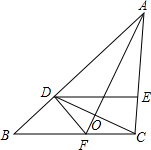 已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.
已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF. 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.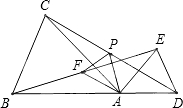 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.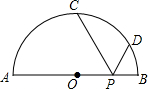 如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.
如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.