题目内容
17.利用一次函数的图象,求方程组$\left\{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}\right.$的解.分析 先利用描点法画出直线y=-2x+4和直线y=x+1,再写出它们的交点坐标,然后根据函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案.
解答 解:画出直线y=-2x+4和直线y=x+1,如图,
它们的交点坐标为(1,2),
所以方程组$\left\{\begin{array}{l}{2x+y=4}\\{x-y=-1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
点评 本题主要考查了函数解析式与图象的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
8.已知有一组数据1,2,m,3,4,其中m是方程$\frac{1}{x-2}$=$\frac{1}{2}$的解,那么这组数据的中位数、众数分别是( )
| A. | 2,2 | B. | 2,3 | C. | 3,4 | D. | 4,4 |
 如图,二次函数y=x(x-2)(0≤x≤2)的图象,记为C1,它与x轴交于O、A1两点;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C2016.若P(4031,m)在第2016段图象C2016上,则m=1.
如图,二次函数y=x(x-2)(0≤x≤2)的图象,记为C1,它与x轴交于O、A1两点;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C2016.若P(4031,m)在第2016段图象C2016上,则m=1.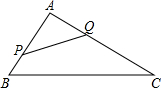 如图,在三角形ABC中,AB=8,AC=16,点P从点B开始沿边BA向点A以2厘米每秒的速度移动,点Q从点A向点C以4厘米每秒的速度移动,如果点P、Q分别从点B、A同时出发,经过多少秒时,以A、P、Q为顶点的三角形与三角形ABC相似?
如图,在三角形ABC中,AB=8,AC=16,点P从点B开始沿边BA向点A以2厘米每秒的速度移动,点Q从点A向点C以4厘米每秒的速度移动,如果点P、Q分别从点B、A同时出发,经过多少秒时,以A、P、Q为顶点的三角形与三角形ABC相似?