题目内容
20.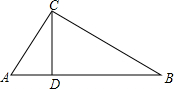 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=32°,CD=6,求AB的长.(结果保留到0.1)(已知sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=32°,CD=6,求AB的长.(结果保留到0.1)(已知sin32°=0.5299,cos32°=0.8480,tan32°=0.6249)
分析 先由CD⊥AB,垂足为D,根据垂直的定义得出∠BDC=90°.解直角△BDC,利用正弦函数的定义得出BC=$\frac{CD}{sin32°}$≈11.32,再解直角△ABC,利用余弦函数的定义得出AB=$\frac{BC}{cos32°}$≈13.3.
解答 解:∵CD⊥AB,垂足为D,
∴∠BDC=90°.
∵在△BDC中,∠BDC=90°,∠B=32°,CD=6,
∴BC=$\frac{CD}{sin32°}$=$\frac{6}{0.5299}$≈11.32,
∵在△ABC中,∠ACB=90°,∠B=32°,BC≈11.32,
∴AB=$\frac{BC}{cos32°}$≈$\frac{11.32}{0.8480}$≈13.3.
点评 本题考查了解直角三角形,锐角三角函数的定义,垂直的定义,求出BC的值是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8.已知有一组数据1,2,m,3,4,其中m是方程$\frac{1}{x-2}$=$\frac{1}{2}$的解,那么这组数据的中位数、众数分别是( )
| A. | 2,2 | B. | 2,3 | C. | 3,4 | D. | 4,4 |
 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=80°,则∠A=50°.
如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠E+∠F=80°,则∠A=50°. 如图,已知平行四边形OABC中,O(0,0),A(-3,-4),B(1,2),求点C的坐标.
如图,已知平行四边形OABC中,O(0,0),A(-3,-4),B(1,2),求点C的坐标.