题目内容
2.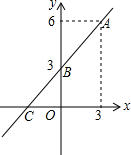 如图,一次函数y=kx+b的图象经过A,B两点,求一次函数的解析式及△AOC的面积.
如图,一次函数y=kx+b的图象经过A,B两点,求一次函数的解析式及△AOC的面积.
分析 由图可知A、B两点的坐标,把两点坐标代入一次函数y=kx+b即可求出k、b的值,进而得出结论;
令y=0,求出点C坐标,由C点坐标可求出OC的长再由A点坐标可知三角形OC边上的高,利用三角形的面积公式即可得出结论.
解答 解:由图象可知点A(3,6)、B(0,3),
将A、B坐标代入一次函数y=kx+b,得:
$\left\{\begin{array}{l}{3k+b=6}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
故一次函数解析式为:y=x+3;
当y=0时,有x+3=0,解得:x=-3,故C点坐标为(-3,0),
S△AOC=$\frac{1}{2}$×OC×yA=$\frac{1}{2}$×3×6=9,
故△AOC面积为9.
点评 本题考查的是待定系数法求一次函数的解析式及一次函数图象上点的坐标特点,先根据一次函数的图象得出A、B、C三点的坐标是解答此题的关键.

练习册系列答案
相关题目
12. 张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
 张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )| A. | 12cm2 | B. | 20cm2 | C. | 24cm2 | D. | 32cm2 |
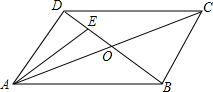 如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.
如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.