��Ŀ����
2��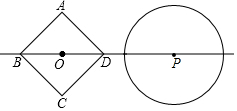 ��ͼ��������ABCD�ı߳�Ϊ$\sqrt{2}$����P�İ뾶Ϊ1��������ABCD������O�͡�P��Բ��P����ֱ��l�ϣ��߶�OP�ij��������ǵ����ľ࣬��P���ŵ�P��ֱ��l�ϵ��˶����˶���
��ͼ��������ABCD�ı߳�Ϊ$\sqrt{2}$����P�İ뾶Ϊ1��������ABCD������O�͡�P��Բ��P����ֱ��l�ϣ��߶�OP�ij��������ǵ����ľ࣬��P���ŵ�P��ֱ��l�ϵ��˶����˶�����1��OD=1��
��2����������ABCD���Pֻ��һ��������ʱ�����ľ�OP=2
��3�����ŵ�P��ֱ��l�ϵ��ƶ���������ABCD���P�Ĺ�����ĸ���������Щ�仯��д����ӦOP��ֵ��ȡֵ��Χ������д��������̣�
���� ��1�����������ε����ʼ��ɵõ����ۣ�
��2����������ABCD���Pֻ��һ��������ʱ�������߶εĺͲ�ɵõ����ۣ�
��3�����ֲ����ɵ�������ABCD���P�Ĺ�����ĸ�����1�������㣬2�������㣬�����ĸ������㣬�ݴ��ҵ���Ӧȡֵ��Χ���ɣ�
���  �⣺��1����������ABCD�ı߳�Ϊ$\sqrt{2}$��
�⣺��1����������ABCD�ı߳�Ϊ$\sqrt{2}$��
��BD=$\sqrt{2}$AB=2��
��OD=2��2=1��
�ʴ�Ϊ��1��
��2����ͼ�����P��ֱ��l����F��E����D��F�غ�ʱ��һ�������㣬OP=1+1=2��
�ʴ�Ϊ��2��
��3��������ABCD���P�Ĺ�����ĸ���������������ʱ��$\frac{1}{2}$��OP��2��
1��������ʱ��OP=2��
���ĸ�������ʱ��0��OP��$\frac{1}{2}$��
���� ���⿼���������κ�Բ�Ķ������⣻�����������εĶԽ�����߳���������ϵ�����ֲ����õ��������α߳����ܵ�����ǽ���������Ҫ������

��ϰ��ϵ�д�
�����Ŀ
12�� ��ͼ���ڡ�ABC�У���ACB=90�㣬BC=3cm��AC=4cm��D��AB���е㣬���Ե�CΪԲ�ģ���3cm��Ϊ�뾶����C��������ѡ���еĵ��ڡ�C����ǣ�������
��ͼ���ڡ�ABC�У���ACB=90�㣬BC=3cm��AC=4cm��D��AB���е㣬���Ե�CΪԲ�ģ���3cm��Ϊ�뾶����C��������ѡ���еĵ��ڡ�C����ǣ�������
 ��ͼ���ڡ�ABC�У���ACB=90�㣬BC=3cm��AC=4cm��D��AB���е㣬���Ե�CΪԲ�ģ���3cm��Ϊ�뾶����C��������ѡ���еĵ��ڡ�C����ǣ�������
��ͼ���ڡ�ABC�У���ACB=90�㣬BC=3cm��AC=4cm��D��AB���е㣬���Ե�CΪԲ�ģ���3cm��Ϊ�뾶����C��������ѡ���еĵ��ڡ�C����ǣ�������| A�� | ��A | B�� | ��B | C�� | ��C | D�� | ��D |
13��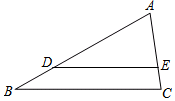 ��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ���DE��BC����AD��DB=3��1��AE=6����AC���ڣ�������
��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ���DE��BC����AD��DB=3��1��AE=6����AC���ڣ�������
 ��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ���DE��BC����AD��DB=3��1��AE=6����AC���ڣ�������
��ͼ���ڡ�ABC�У���D��E�ֱ���AB��AC���ϣ���DE��BC����AD��DB=3��1��AE=6����AC���ڣ�������| A�� | 3 | B�� | 4 | C�� | 6 | D�� | 8 |
10��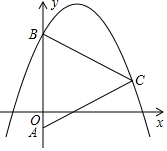 ��ͼ����֪������y=-$\frac{2}{3}$x2+$\sqrt{3}$x+3��ͼ����y�ύ�ڵ�B����C���������ڵ�һ�����ϵ�һ���㣬����BCΪ��������ABC��y���ڵ�A�����A������Ϊ��������
��ͼ����֪������y=-$\frac{2}{3}$x2+$\sqrt{3}$x+3��ͼ����y�ύ�ڵ�B����C���������ڵ�һ�����ϵ�һ���㣬����BCΪ��������ABC��y���ڵ�A�����A������Ϊ��������
 ��ͼ����֪������y=-$\frac{2}{3}$x2+$\sqrt{3}$x+3��ͼ����y�ύ�ڵ�B����C���������ڵ�һ�����ϵ�һ���㣬����BCΪ��������ABC��y���ڵ�A�����A������Ϊ��������
��ͼ����֪������y=-$\frac{2}{3}$x2+$\sqrt{3}$x+3��ͼ����y�ύ�ڵ�B����C���������ڵ�һ�����ϵ�һ���㣬����BCΪ��������ABC��y���ڵ�A�����A������Ϊ��������| A�� | ��-1��0�� | B�� | ��-$\sqrt{3}$��0�� | C�� | ��0��1�� | D�� | ��0��$\sqrt{3}$�� |
7��С�����ü���������һ����������������������������
��ô����������Ϊ100ʱ�����������Ϊ��������
| ������ | �� | 1 | 2 | 3 | 4 | 5 | �� |
| ����� | �� | -4 | -1 | 2 | 5 | 8 | �� |
| A�� | 293 | B�� | 296 | C�� | 297 | D�� | 300 |
11������a2bm��n�������ȷ���ǣ�������
| A�� | a2nbmn | B�� | a${\;}^{{n}^{2}}$b${\;}^{{m}^{n}}$ | C�� | a${\;}^{{n}^{2}}$bmn | D�� | a2nb${\;}^{{m}^{n}}$ |
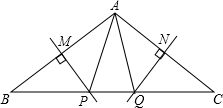 ��ͼ��ʾ��MP�� NQ�ֱ�ֱƽ��AB ��AC��
��ͼ��ʾ��MP�� NQ�ֱ�ֱƽ��AB ��AC��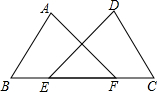 ��ͼ����E��F���߶�BC����F��E���Ҳ࣬BE=CF��AB=DC����B=��C����֤����A=��D��
��ͼ����E��F���߶�BC����F��E���Ҳ࣬BE=CF��AB=DC����B=��C����֤����A=��D��