题目内容
6. 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )| A. | $\frac{2013×2012}{4}$ | B. | $\frac{2013×2012}{2}$ | C. | $\frac{503×2013}{2}$ | D. | $\frac{2012×2011}{4}$ |
分析 S1、S2、…、S2012中,所有三角形在y轴上的直角边都是1,因此只需考虑它们的另一条直角边即可;也可以看作,这些三角形面积的平方和等于所有Q点横坐标的平方和,可先表示出点Q的横坐标的平方,结合等差数列即可求出代数式的值.
解答 解:设点Q($\sqrt{2013-y}$,y);(0<y<2013)
那么 Qn($\sqrt{2013-n}$,n).(1≤n≤2012)
S12=$\frac{1}{4}$(2013-1)=$\frac{1}{4}$×2012
S22=$\frac{1}{4}$(2013-2)=$\frac{1}{4}$×2011
S32=$\frac{1}{4}$(2013-3)=$\frac{1}{4}$×2010
…
S20122=$\frac{1}{4}$(2013-2012)=$\frac{1}{4}$×1
∴S12+S22+S32+…+S20122=$\frac{1}{4}$(2012+2011+2010+…+1)=$\frac{1}{4}$×$\frac{2012(2012+1)}{2}$=$\frac{503×2013}{2}$
故选C.
点评 此题的难度适中,把握住每个直角三角形一条直角边都是1是解答题目的关键,此外,还需牢记等差数列的求和公式Sn=$\frac{n({a}_{1}+{a}_{n})}{2}$.

练习册系列答案
相关题目
 如图,P、Q是反比例函数图象上两点,且关于原点对称,QE⊥x轴,矩形PEQF的面积是3,则反比例函数的表达式为y=-$\frac{3x}{4}$.
如图,P、Q是反比例函数图象上两点,且关于原点对称,QE⊥x轴,矩形PEQF的面积是3,则反比例函数的表达式为y=-$\frac{3x}{4}$.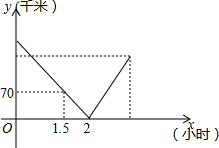 一辆中巴车和一辆大巴车分别从甲、乙两站出发,匀速相向而行,相遇后继续前行,已知两车相遇时中巴比大巴多行驶40千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至中巴到达乙站这一过程中y与x之间的函数关系.根据图象提供的信息,可知:当中巴到达乙站时,大巴离甲站的距离为70千米.
一辆中巴车和一辆大巴车分别从甲、乙两站出发,匀速相向而行,相遇后继续前行,已知两车相遇时中巴比大巴多行驶40千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至中巴到达乙站这一过程中y与x之间的函数关系.根据图象提供的信息,可知:当中巴到达乙站时,大巴离甲站的距离为70千米.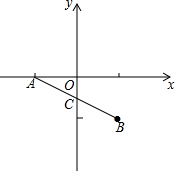 如图,已知A(-2,0),B(2,-2),线段AB交y轴于点C.
如图,已知A(-2,0),B(2,-2),线段AB交y轴于点C.