题目内容
如图，已知⊙O1的半径为6cm，⊙O2的半径为8cm，O1O2=10cm，两圆交于A、B两点，求AB的长．考点：相交两圆的性质
专题：
分析：如图，作辅助线，得到两个直角△O1BC、△O2BC；根据勾股定理列出关于线段BC的方程，求出BC的长度即可解决问题．
解答：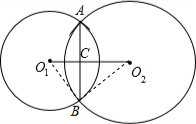
解：如图，连接O1B、O2B；
∵两圆交于A、B两点，
∴O1O2⊥AB，且BC=AC；
设O1C=λ，则O2C=10-λ；
由勾股定理得：
BC2=O1B2-O1C2，BC2=O2B2-O2C2，
∴62-λ2=82-（10-λ）2，
解得：λ=
，
∴BC2=36-
，
∴BC=
，AB=2BC=
．
解：如图，连接O1B、O2B；∵两圆交于A、B两点，
∴O1O2⊥AB，且BC=AC；
设O1C=λ，则O2C=10-λ；
由勾股定理得：
BC2=O1B2-O1C2，BC2=O2B2-O2C2，
∴62-λ2=82-（10-λ）2，
解得：λ=
| 18 |
| 5 |
∴BC2=36-
| 324 |
| 25 |
∴BC=
| 24 |
| 5 |
| 48 |
| 5 |
点评：该题主要考查了相交两圆的性质及其应用问题；解题的关键是作辅助线，灵活运用勾股定理等几何知识点来分析、判断、推理或解答；对运算求解能力也提出了一定的要求．
练习册系列答案
相关题目
为丰富学生的业余生活，培养学生的兴趣和爱好，某区各个学校开展了学生社团活动，为了解学生参加社团活动情况，对某校七年级学生社团活动进行了抽样调查，制作出如下的统计图，已知该学校七年级学生每人都根据爱好参加一项社团活动．
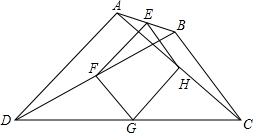在四边形ABCD中，E、F、G、H分别是AB、BD、DC、AC的中点．