题目内容
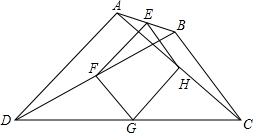 在四边形ABCD中,E、F、G、H分别是AB、BD、DC、AC的中点.
在四边形ABCD中,E、F、G、H分别是AB、BD、DC、AC的中点.(1)求证:四边形EFGH是平行四边形;
(2)若四边形EFGH是矩形,求证:∠ADC+∠BCD=90°.
考点:中点四边形
专题:证明题
分析:(1)利用三角形中位线定理得出EF=
AD,FG=
BC,GH=
AD,HE=
BC,进而求出即可;
(2)利用矩形的性质∠ADC+∠BCD=∠HGC+∠FGD,进而求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用矩形的性质∠ADC+∠BCD=∠HGC+∠FGD,进而求出即可.
解答:证明:(1)∵E、F、G、H分别是AB、BD、DC、AC的中点,
∴EF、FG、GH、HE分别是△ABD、△BDC、△ADC、△ABC的中位线,
∴EF=
AD,FG=
BC,GH=
AD,HE=
BC,
∴EF=GH,FG=EH,
∴四边形EFGH是平行四边形;
(2)由(1)可得,FG∥BC,GH∥AD,
故∠ADC=∠HGC,∠BCD=∠FGD,
∵四边形EFGH是矩形,∴∠FGH=90°,
∴∠ADC+∠BCD=∠HGC+∠FGD=180°-∠FGH=90°.
∴EF、FG、GH、HE分别是△ABD、△BDC、△ADC、△ABC的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=GH,FG=EH,
∴四边形EFGH是平行四边形;
(2)由(1)可得,FG∥BC,GH∥AD,
故∠ADC=∠HGC,∠BCD=∠FGD,
∵四边形EFGH是矩形,∴∠FGH=90°,
∴∠ADC+∠BCD=∠HGC+∠FGD=180°-∠FGH=90°.
点评:此题主要考查了中点四边形的性质以及平行四边形和矩形的判定,正确把握相关性质是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知⊙O1的半径为6cm,⊙O2的半径为8cm,O1O2=10cm,两圆交于A、B两点,求AB的长.
如图,已知⊙O1的半径为6cm,⊙O2的半径为8cm,O1O2=10cm,两圆交于A、B两点,求AB的长. 如图是由小正方体组成的立体图的俯视图,数字表示小正方体的个数,请画出该立体图的主视图和左视图.
如图是由小正方体组成的立体图的俯视图,数字表示小正方体的个数,请画出该立体图的主视图和左视图.