题目内容
17. 将一副三角尺拼图,并标点描线如图所示,然后过点C作CF平分∠DCE,交DE于点F.
将一副三角尺拼图,并标点描线如图所示,然后过点C作CF平分∠DCE,交DE于点F.(1)求证:CF∥AB;
(2)求∠EFC的度数.
分析 (1)根据内错角相等,两直线平行进行判定即可;
(2)根据三角形EFC的内角和为180°,求得∠EFC的度数.
解答  解:(1)∵CF平分∠DCE,且∠DCE=90°,
解:(1)∵CF平分∠DCE,且∠DCE=90°,
∴∠ECF=45°,
∵∠BAC=45°,
∴∠BAC=∠ECF,
∴CF∥AB;
(2)在△FCE中,
∵∠FCE+∠E+∠EFC=180°,
∴∠EFC=180°-∠FCE-∠E,
=180°-45°-30°
=105°.
点评 本题主要考查了平行线的判定以及三角形内角和定理的运用,解题时注意:内错角相等,两直线平行.解题的关键是熟知三角板的各角度数.

练习册系列答案
相关题目
7. 如图所示的圆锥,它的主视图和俯视图分别是( )
如图所示的圆锥,它的主视图和俯视图分别是( )
 如图所示的圆锥,它的主视图和俯视图分别是( )
如图所示的圆锥,它的主视图和俯视图分别是( )| A. | 等边三角形、圆 | B. | 等边三角形、等腰三角形 | ||
| C. | 等腰三角形、圆 | D. | 圆、等腰三角形 |
 如图,边长为$\sqrt{3}$的正六边形ABCDEF的顶点A、B在圆O上,顶点C、D、E、F在该圆内,∠AOB=36°,将正六边形ABCDEF绕点A逆时针旋转,当点F第一次落在圆上时,点E运动的路线长是$\frac{2}{5}$π(结果保留π).
如图,边长为$\sqrt{3}$的正六边形ABCDEF的顶点A、B在圆O上,顶点C、D、E、F在该圆内,∠AOB=36°,将正六边形ABCDEF绕点A逆时针旋转,当点F第一次落在圆上时,点E运动的路线长是$\frac{2}{5}$π(结果保留π). 如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?
如图,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应滑动多少米?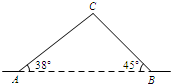 如图,从A地到B地的公路需经过C地,AC=10千米,∠CAB=38°,∠ABC=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直后的公路AB的长(精确到1千米).(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78)
如图,从A地到B地的公路需经过C地,AC=10千米,∠CAB=38°,∠ABC=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.求改直后的公路AB的长(精确到1千米).(参考数据:sin38°=0.62,cos38°=0.79,tan38°=0.78)