题目内容
3.计算或化简:(1)计算:2-1-$\sqrt{3}$tan60°+(π-2011)0+|-$\frac{1}{2}$|.
(2)化简:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$.
分析 (1)分别利用绝对值以及零指数幂的性质和特殊角的三角函数值化简求出即可;
(2)首先将括号里面通分,进而分解因式化简求出即可.
解答 解:(1)2-1-$\sqrt{3}$tan60°+(π-2011)0+|-$\frac{1}{2}$|
=$\frac{1}{2}$-$\sqrt{3}$×$\sqrt{3}$+1+$\frac{1}{2}$
=$\frac{1}{2}$-3+1+$\frac{1}{2}$
=-1;
(2)(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$
=$\frac{x-1}{x}$×$\frac{(x+1)(x-1)}{(x-1)^{2}}$
=$\frac{x+1}{x}$.
点评 此题主要考查了绝对值以及零指数幂的性质和特殊角的三角函数值以及分式的混合运算,正确分解因式是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
11.已知样本x1,x2,x3,…,xn的平均数是3,方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的平均数和方差是( )
| A. | 3,1 | B. | 3,2 | C. | 9,3 | D. | 9,4 |
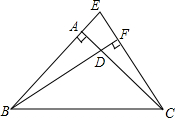 如图,在△ABC中,∠BAC=90°,AB=AC,E是BA的延长线上,连接CE,BF⊥CE交AC于D,垂足为F,求证:BD=CE.
如图,在△ABC中,∠BAC=90°,AB=AC,E是BA的延长线上,连接CE,BF⊥CE交AC于D,垂足为F,求证:BD=CE.
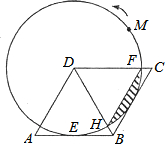 如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.