题目内容
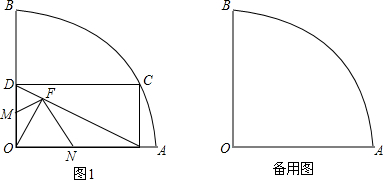
如图,扇形OAB的半径为4,圆心角∠AOB=90?,点C是
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
(1)当tan∠MOF=
时,求
的值;
(2)设OM=x,ON=y,当
=
时,求y关于x的函数解析式,并写出它的定义域;
(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.
 |
| AB |
(1)当tan∠MOF=
| 1 |
| 3 |
| OM |
| NE |
(2)设OM=x,ON=y,当
| OM |
| OD |
| 1 |
| 2 |
(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.

考点:圆的综合题
专题:
分析:(1)在直角三角形中由OF2=DF•FE和tan∠MOF=
,得出DF=
OF,所以OF2=
OF•FE,即
=
,再由△OMF∽△ENF,得出
=
,
(2)连接MN,设OM=x,ON=y,△OFD是直角三角形,由已知得出OM=MD=MF=x,因为∠MON=∠MFN=90°,得出MN是∠ONE的角平分线,MN是OF的中垂线,求出∠NEF=∠NFE,
得出ON=NE=NF=y,在RT△DOE中,运用勾股定理OD2+OE2=DE2,求得(2x)2+(2y)2=42,即y2=4-x2(0<x≤2),
(3)分两种情况①由△ECF∽△OFN,得出
=
,利用△DOE的面积,
OE•OD=
DE•OF解得,OF=xy,求出EF,由(2)y2=4-x2得出
=
解得,y=
,再求出x=
,所以OD=2x=2
②由△ECF∽△ONF,得OD=
.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| OF |
| FE |
| 1 |
| 3 |
| OM |
| NE |
| 1 |
| 3 |
(2)连接MN,设OM=x,ON=y,△OFD是直角三角形,由已知得出OM=MD=MF=x,因为∠MON=∠MFN=90°,得出MN是∠ONE的角平分线,MN是OF的中垂线,求出∠NEF=∠NFE,
得出ON=NE=NF=y,在RT△DOE中,运用勾股定理OD2+OE2=DE2,求得(2x)2+(2y)2=42,即y2=4-x2(0<x≤2),
(3)分两种情况①由△ECF∽△OFN,得出
| OF |
| ON |
| EC |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| xy |
| y |
| 2x |
| y2 |
| 2 |
| 2 |
| 2 |
4
| ||
| 3 |
解答:
解;(1)如图1,∵∠AOB=90?,CE⊥OA,CD⊥OB,
∴四边形ACDO是矩形,
∴DE=OC=4,
∵OF⊥DE,
∴OF2=DF•FE
∵tan∠MOF=
,
∴
=
,即DF=
OF,
∴OF2=
OF•FE,即
=
,
∵∠MFO+∠OFN=∠NFE+∠OFN=90°,
∴∠MFO=∠NFE,
∵∠MOF+∠ODE=∠NEF+∠ODE=90°,
∴∠MOF=∠NEF,
∴△OMF∽△ENF,
∴
=
=
,即
=
,
(2)如图2,连接MN,

设OM=x,ON=y,
∵
=
,即OD=2OM,△OFD是直角三角形,
∴OM=MD=MF=x,
∵∠MON=∠MFN=90°,
∴MN是∠ONF的角平分线,
∴MN是OF的中垂线,
∴ON=NF,可得∠FON=∠NFO
∵∠FON+∠NEF=∠NFO+∠NFE,
∴∠NEF=∠NFE,
∴ON=NE=NF=y,
∵DE=OC=4,
在RT△DOE中,OD2+OE2=DE2
∴(2x)2+(2y)2=42,即y2=4-x2(0<x≤2),
(3)如图3,

①∵△ECF∽△OFN
∴
=
,
利用△DOE的面积,
OE•OD=
DE•OF
∵OD=2x,OE=2y,DE=4,
∴
×2y×2x=
×4•OF,
解得,OF=xy,
∵OE=2y,
∴EF=
=
=y
,
由(2)y2=4-x2
∴EF=y2,
∵CE=OD=2x,
∴
=
解得,y=
,
代入x2+y2=4,得x=
,
∴OD=2x=2
.
②∵△ECF∽△ONF
∴
=
,
利用△DOE的面积,
OE•OD=
DE•OF
∵OD=2x,OE=2y,DE=4,
∴
×2y×2x=
×4•OF,
解得,OF=xy,
∵OE=2y,
∴EF=
=
=y
,
由(2)y2=4-x2
∴EF=y2,
∵CE=OD=2x,
∴
=
,
解得,y=
x,
代入x2+y2=4,得x=
,
∴OD=2x=
.
综上所述OD的长为2
或
.

解;(1)如图1,∵∠AOB=90?,CE⊥OA,CD⊥OB,
∴四边形ACDO是矩形,
∴DE=OC=4,
∵OF⊥DE,
∴OF2=DF•FE
∵tan∠MOF=
| 1 |
| 3 |
∴
| DF |
| OF |
| 1 |
| 3 |
| 1 |
| 3 |
∴OF2=
| 1 |
| 3 |
| OF |
| FE |
| 1 |
| 3 |
∵∠MFO+∠OFN=∠NFE+∠OFN=90°,
∴∠MFO=∠NFE,
∵∠MOF+∠ODE=∠NEF+∠ODE=90°,
∴∠MOF=∠NEF,
∴△OMF∽△ENF,
∴
| OM |
| NE |
| OF |
| EF |
| 1 |
| 3 |
| OM |
| NE |
| 1 |
| 3 |
(2)如图2,连接MN,

设OM=x,ON=y,
∵
| OM |
| OD |
| 1 |
| 2 |
∴OM=MD=MF=x,
∵∠MON=∠MFN=90°,
∴MN是∠ONF的角平分线,
∴MN是OF的中垂线,
∴ON=NF,可得∠FON=∠NFO
∵∠FON+∠NEF=∠NFO+∠NFE,
∴∠NEF=∠NFE,
∴ON=NE=NF=y,
∵DE=OC=4,
在RT△DOE中,OD2+OE2=DE2
∴(2x)2+(2y)2=42,即y2=4-x2(0<x≤2),
(3)如图3,

①∵△ECF∽△OFN
∴
| OF |
| ON |
| EC |
| EF |
利用△DOE的面积,
| 1 |
| 2 |
| 1 |
| 2 |
∵OD=2x,OE=2y,DE=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得,OF=xy,
∵OE=2y,
∴EF=
| OE2-OF2 |
| 4y2-(xy)2 |
| 4-x2 |
由(2)y2=4-x2
∴EF=y2,
∵CE=OD=2x,
∴
| xy |
| y |
| 2x |
| y2 |
解得,y=
| 2 |
代入x2+y2=4,得x=
| 2 |
∴OD=2x=2
| 2 |
②∵△ECF∽△ONF
∴
| EC |
| ON |
| EF |
| OF |
利用△DOE的面积,
| 1 |
| 2 |
| 1 |
| 2 |
∵OD=2x,OE=2y,DE=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得,OF=xy,
∵OE=2y,
∴EF=
| OE2-OF2 |
| 4y2-(xy)2 |
| 4-x2 |
由(2)y2=4-x2
∴EF=y2,
∵CE=OD=2x,
∴
| 2x |
| y |
| y2 |
| xy |
解得,y=
| 2 |
代入x2+y2=4,得x=
2
| ||
| 3 |
∴OD=2x=
4
| ||
| 3 |
综上所述OD的长为2
| 2 |
4
| ||
| 3 |
点评:本题主要考查了圆的综合题,解本题关键是把圆的知识和相似三角形的知识相结合求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当x为任意实数时,下列分式一定有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
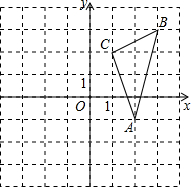 如图,平面直角坐标系中,△ABC的顶点都在网格点上.
如图,平面直角坐标系中,△ABC的顶点都在网格点上.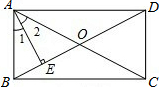 如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,AB=2cm.
如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,AB=2cm.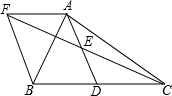 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且BD=DC,连接BF,求证:四边形AFBD为平行四边形.
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且BD=DC,连接BF,求证:四边形AFBD为平行四边形. 如图,已知半径为2的⊙O与直线x相切于点A,点P 是直径AB左侧半圆上的动点,过点P作直线x的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4).
如图,已知半径为2的⊙O与直线x相切于点A,点P 是直径AB左侧半圆上的动点,过点P作直线x的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4).