题目内容
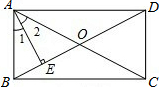 如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,AB=2cm.
如图,矩形ABCD的对角线AC、BD相交于点O,AE⊥BD,垂足为E,∠1=∠2,AB=2cm.(1)求∠BAC的度数;
(2)求BC的长.
考点:矩形的性质
专题:
分析:(1)利用矩形的性质和直角三角形的性质推知∠1=∠2=∠ACB=30°,则∠BAC=90°-30°=60°;
(2)通过解直角△ABC来求线段BC的长度.
(2)通过解直角△ABC来求线段BC的长度.
解答: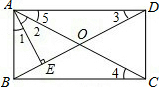 解:(1)如图,在矩形ABCD中,∠BAD=90°,∠3=∠4=∠5
解:(1)如图,在矩形ABCD中,∠BAD=90°,∠3=∠4=∠5
∵AE⊥BD,
∴∠1=∠3,
又∵∠1=∠2,
∴∠1=∠2=∠3=∠4=∠5,
∴∠2+∠5+∠3=90°,即3∠3=90°
∴∠3=30°,
∴∠1+∠2=60°,即∠BAC=60°;
(2)由(1)知,∠BAC=60°.
∵AB=2cm,
∴BC=AB•tan60°=2
,即BC的长度是2
cm.
 解:(1)如图,在矩形ABCD中,∠BAD=90°,∠3=∠4=∠5
解:(1)如图,在矩形ABCD中,∠BAD=90°,∠3=∠4=∠5∵AE⊥BD,
∴∠1=∠3,
又∵∠1=∠2,
∴∠1=∠2=∠3=∠4=∠5,
∴∠2+∠5+∠3=90°,即3∠3=90°
∴∠3=30°,
∴∠1+∠2=60°,即∠BAC=60°;
(2)由(1)知,∠BAC=60°.
∵AB=2cm,
∴BC=AB•tan60°=2
| 3 |
| 3 |
点评:本题考查了矩形的性质.此题利用了矩形的对角线互相平分且相等、内角为直角的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式运算正确的是( )
| A、a•a4=a5 |
| B、2a3÷a=2a |
| C、(2x2)3=6x6 |
| D、3x2-x2=x2 |
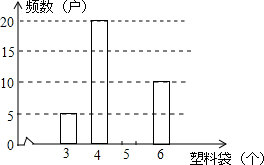 为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).
为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).

 如图,在四边形ABCD中,∠B=∠D,AD∥BC,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=∠D,AD∥BC,求证:四边形ABCD是平行四边形. 如图,反比例函数y=
如图,反比例函数y=