题目内容
9.如图,在直角坐标系中,已知点A(-4,0),B(0,3),对△OAB连续作旋转变换,依次得到三角形(1),三角形(2),三角形(3),三角形(4),…,则三角形(2016)的直角顶点的坐标是(8064,0).
分析 先利用勾股定理计算出AB,从而得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2016=3×672,于是可判断三角形2016与三角形1位置一样,然后计算672×12即可得到三角形2016的直角顶点坐标.
解答 解:∵A(-3,0),B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴△ABC的周长=3+4+5=12,
∵△OAB每连续3次后与原来的状态一样,
∵2016=3×672,
∴三角形2016与三角形1的状态一样,
∴三角形2016的直角顶点的横坐标=672×12=8064,
∴三角形2016的直角顶点坐标为(8064,0).
故答案为(8064,0).
点评 本题考查了坐标与图形变化-旋转,图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.解决本题的关键是确定循环的次数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°,则∠ADC=125°.
如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°,则∠ADC=125°. 如图,过正六边形ABCDEF的顶点A作直线l∥CE,则∠1=30°.
如图,过正六边形ABCDEF的顶点A作直线l∥CE,则∠1=30°.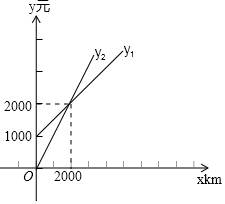 某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,付给出租车公司的月租费是y2元,y1,y2分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题:
某单位需要用车,准备和一个体车主或一国有出租公司其中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,付给出租车公司的月租费是y2元,y1,y2分别与x之间的函数关系图象是如图所示的两条直线,观察图象,回答下列问题: 光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射,如图,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.若水面和杯底是互相平行的,且∠1=45°,∠2=122°,则∠3=45°,∠4=58°.
光线在不同介质中的传播速度不同,因此当光线从水中射向空气时,要发生折射,如图,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.若水面和杯底是互相平行的,且∠1=45°,∠2=122°,则∠3=45°,∠4=58°.