题目内容
6.能否将正整数1,2,3,…,33分成3个一组的数共11组,使得每组数中都有一个数等于其余两个数之和.分析 利用反证法,设第一个组为a,b,c且a+b=c,知第一个组的和为2c,为偶数,即可知所有数的和为偶数,而1+2+…+33为奇数,即可得答案.
解答 解:假设有这样的分组使每组数中都有一个数等于其余两个数之和,
设第一个组为a,b,c,且a+b=c,
则第一个组的和为2c,为偶数,
依此类推,其他11个组的和也都是偶数,最后11个组的和应该是偶数,
∵1+2+3+…+33=$\frac{(1+33)×33}{2}$=561,不是偶数,
∴假设是错误的,即不存在这样的分组使每组数中都有一个数等于其余两个数之和.
点评 本题主要考查数字的变化类和反证法,根据题意得出每个分组的数字之和为偶数是解题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
14.下列事件中是必然事件的是( )
| A. | a 是实数,|a|≥0 | |
| B. | 打开数学课本时刚好翻到第60页 | |
| C. | 从一定高度落下的图钉,落地后钉尖朝上 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出白球 |
12.下列事件中,属于不可能事件的是( )
| A. | 投出的篮球会下落 | B. | 从装有黑球、白球的袋里摸出红球 | ||
| C. | 367人中至少有2人是同月同日出生 | D. | 买1张彩票,中500万大奖 |

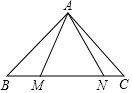 如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,点M、N在边BC上,且∠MAN=45°,CN=5,MN=13.
如图,在等腰直角三角形ABC中,∠BAC=90°,AB=AC=15$\sqrt{2}$,点M、N在边BC上,且∠MAN=45°,CN=5,MN=13.