题目内容
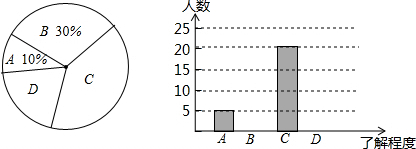
低碳发展正在试行，小聪同学就本班学生对低碳知识的了解程度惊醒了一次调查统计，如图是他采集数据后绘制的两幅不完整的统计图（A．不了解，B．一般了解，C．了解较多，D．熟悉）．请你根据图中提供的信息解答以下问题：
（1）求该班共有多少名学生？
（2）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数．
（3）若该班A类5名学生中有3男2女，从中随机抽取2名学生，请用列表法或树状图求抽取的2名学生恰好是1男1女的概率．
（1）求该班共有多少名学生？
（2）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数．
（3）若该班A类5名学生中有3男2女，从中随机抽取2名学生，请用列表法或树状图求抽取的2名学生恰好是1男1女的概率．
考点：列表法与树状图法,扇形统计图,条形统计图
专题：计算题
分析：（1）根据A的人数除以占的百分比求出班级学生总数即可；
（2）求出C占的百分比，乘以360即可得到结果；
（3）列表得出所有等可能的情况数，找出抽取的2名学生恰好是1男1女的情况数，即可求出所求的概率．
（2）求出C占的百分比，乘以360即可得到结果；
（3）列表得出所有等可能的情况数，找出抽取的2名学生恰好是1男1女的情况数，即可求出所求的概率．
解答：解：（1）根据题意得：5÷10%=50（人），
则该班学生数为50人；
（2）根据题意得：“了解较多”部分所对应的圆心角的度数为
×360°=144°；
（3）列表如下：
所有等可能的情况有20种，其中抽取的2名学生恰好是1男1女的情况有12种，
则P=
=
．
则该班学生数为50人；
（2）根据题意得：“了解较多”部分所对应的圆心角的度数为
| 20 |
| 50 |
（3）列表如下：
| 男 | 男 | 男 | 女 | 女 | |
| 男 | --- | （男，男） | （男，男） | （女，男） | （女，男） |
| 男 | （男，男） | --- | （男，男） | （女，男） | （女，男） |
| 男 | （男，男） | （男，男） | --- | （女，男） | （女，男） |
| 女 | （男，女） | （男，女） | （男，女） | --- | （女，女） |
| 女 | （男，女） | （男，女） | （男，女） | （女，女） | --- |
则P=
| 12 |
| 20 |
| 3 |
| 5 |
点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，已知抛物线y=x2-x-6，与x轴交于点A和B，点A在点B的左边，与y轴的交点为C．
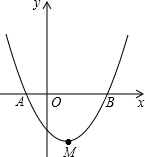如图，二次函数y=
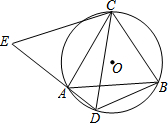如图，△ABC是⊙O的内接三角形，AC=BC，点D是⊙O中弧AB的上的一点，延长DA至点E，使CE=CD．
某校开展学年“好书伴我成长”读书活动，为了解全校1500名学生的读书情况，随机调查了部分学生读数的册数，统计数据如下表所示，并绘制了如下统计图．