题目内容
在矩形ABCD中，AB=4，AD=8，点P为对角线BD垂直平分线上一点，且PD=5，则AP的长是 ．
考点：矩形的性质,线段垂直平分线的性质,勾股定理
专题：计算题
分析：根据题意画出图形，如图所示，利用线段垂直平分线定理得到BM=DM，可得出AM+BM=AM+MD=AD=8，设AM=x，则有BM=8-x，在直角三角形ABM中，利用勾股定理列出关于x的方程，求出方程的解得到AM与DM的长，根据DM=5，得到此时P与M重合，AP的长即为AM的长；当P与N重合时，在直角三角形ABN中，由AB与BN的长，利用勾股定理求出AN的长即为AP的长．
解答：
解：连接矩形ABCD对角线BD，做出BD的垂直平分线MN，交AD、BC分别于M，N点，连接BM，DN，AN，
∴BM=MD，AM+MD=AM+BM=AD=8，
在Rt△ABM中，设AM=x，BM=8-x，AB=4，
根据勾股定理得：x2+42=（8-x）2，
解得：x=3，
∴AM=3，MD=5，
当P与M重合时，PD=5，此时AP=3；
连接AN，当P与N重合时，由对称性得到PD=ND=BN=5，
在Rt△ABN中，AB=4，BN=5，
根据勾股定理得：AN=
=
，此时AP=
．
故答案为：3或
．
解：连接矩形ABCD对角线BD，做出BD的垂直平分线MN，交AD、BC分别于M，N点，连接BM，DN，AN，∴BM=MD，AM+MD=AM+BM=AD=8，
在Rt△ABM中，设AM=x，BM=8-x，AB=4，
根据勾股定理得：x2+42=（8-x）2，
解得：x=3，
∴AM=3，MD=5，
当P与M重合时，PD=5，此时AP=3；
连接AN，当P与N重合时，由对称性得到PD=ND=BN=5，
在Rt△ABN中，AB=4，BN=5，
根据勾股定理得：AN=
| 42+52 |
| 41 |
| 41 |
故答案为：3或
| 41 |
点评：此题考查了矩形的性质，线段垂直平分线定理，以及勾股定理，熟练掌握矩形的性质是解本题的关键．
练习册系列答案
一线名师权威作业本系列答案
相关题目
如图，小丽想知道自家门前小河的宽度，于是她按以下办法测出了如下数据：小丽在河岸边选取点A，在点A的对岸选取一个参照点C，测得∠CAD=30°；小丽沿岸向前走30m选取点B，并测得∠CBD=60°．请根据以上数据，用你所学的数学知识，帮小丽计算小河的宽度．
如图，函数y=kx和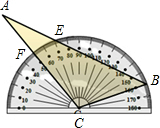
将量角器按如图所示的方式放置在三角形纸片上，使点C在半圆圆心上，点B在半圆上，边AB、AC分别交圆于点E、F，点B、E、F对应的读数分别为160°、70°、50°，则∠A的度数为
如图是由八个相同小正方体组合而成的几何体，则其俯视图是（ ）A、 |
B、 |
C、 |
D、 |
下列命题中，正确的是（ ）
| A、相等的角是对顶角 |
| B、等腰三角形都相似 |
| C、位似图形上任意一对对应点到位似中心的距离之比等于位似比 |
| D、对角线互相垂直平分的四边形是正方形 |
