题目内容
18.某学校计划租用7辆客车送八年级师生去秋游,现有甲、乙两种型号客车,它们的载客量和租金如表,设租用甲种客车x辆.| 甲种客车 | 乙种客车 | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 500 | 320 |
(2)租车总费用为y元.求出y(元)与x(辆)之间的函数关系式;指出自变量的取值范围;
(3)若该校八年级师生共有254名师生参加这次秋游,甲种客车不多于5辆,问:有几种可行的租车方案?哪种方案租车费最省?
分析 (1)租用乙种客车(7-x)辆,分别表示出两种车的载客量,然后求和即可;
(2)设租用甲种客车x辆,则租用乙种客车(7-x)辆,租用甲种客车的费用为500x元,租用乙种客车的费用为320(7-x)元,租车总费用就等于两种租车费用之和;
(3)根据题意列出不等式组,求出不等式组的解救可以确定租车方案,再根据(1)的解析式就可以求出最节省的方案.
解答 解:(1)租用乙种客车(7-x)辆,则W=45x+30(7-x),即W=15x+210.
故答案是:W=15x+210;
(2)设租用甲种客车x辆,则租用乙种客车(7-x)辆,根据题意得租车总费用为y元.
则y=500x+320(7-x)=180x+2240 (0≤x≤7且x为整数);
(3)根据题意列不等式组得:$\left\{\begin{array}{l}{45x+30(7-x)≥254}\\{500x+320(7-x)≤3000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x≥\frac{44}{15}}\\{x≤\frac{38}{9}}\end{array}\right.$,
∵x为整数,
∴x可取的值为3、4,
∴可行的租车方案有两种:3辆45座,4辆30座的,或4辆45座3辆30座的.
∵3×500+4×320=2780,4×500+320×3=2960>2780
∴第一种方案租用3辆45座,4辆30座的能使租车费用剩余最多.
点评 本题考查了运用一次函数解实际问题的运用,一元一次不等式组解实际问题的运用,方案设计的运用,在解答时运用一次函数的性质求解是关键.

练习册系列答案
相关题目
8.若a,b互为相反数(a≠0),则关于x的方程ax+b=0的解是( )
| A. | x=1 | B. | x=-1 | C. | x=1或x=-1 | D. | 不能确定 |
9.一只不透明的袋子中装有4个质地,大小均相同的小球,这些小球分别标有3,4,5,x,甲,乙两人每次同时从袋中各随机取出1个小球,并计算两个小球数字之和.记录后将小球放回袋中搅匀.进行重复实验,实验数据如表:
解答下列问题:
(1)如果实验继续进行下去,根据上表提供数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是.
(2)如果摸出这两个小球上数字之和为9的概率是$\frac{1}{3}$,那么x的值可以取7吗?请用列表或画树状图的方法说明理由.
| 摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
| “和为8“出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
| “和为8“出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
(1)如果实验继续进行下去,根据上表提供数据,出现和为8的频率将稳定在它的概率附近,估计出现和为8的概率是.
(2)如果摸出这两个小球上数字之和为9的概率是$\frac{1}{3}$,那么x的值可以取7吗?请用列表或画树状图的方法说明理由.
10.一个角的补角与这个角的余角的差是( )
| A. | 锐角 | B. | 直角 | ||
| C. | 钝角 | D. | 以上三种都有可能 |
7.若x2+y2=10,xy=3,则x+y的值为( )
| A. | 12 | B. | 4 | C. | -4 | D. | ±4 |
8.点(-3,2)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
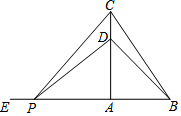 如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.
如图,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,点D在线段AC上,且CD=1 cm,动点P从BA的延长线上距A点5 cm的E点出发,以每秒2 cm的速度沿射线EA的方向运动了t秒.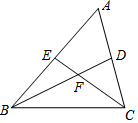 如图,BD、CE是ABC的两条中线,它们相交于点F,请写出EF:CF的值,并说明理由.
如图,BD、CE是ABC的两条中线,它们相交于点F,请写出EF:CF的值,并说明理由.