题目内容
3.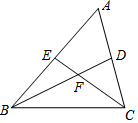 如图,BD、CE是ABC的两条中线,它们相交于点F,请写出EF:CF的值,并说明理由.
如图,BD、CE是ABC的两条中线,它们相交于点F,请写出EF:CF的值,并说明理由.
分析 过点C作CG∥AB交BD的延长线于点G,从而可证明△ABD≌△CGD(AAS),所以AB=CG,由于BE∥CG,所以△BEF∽△GCF,从而可知$\frac{BE}{CG}=\frac{EF}{CF}$=$\frac{1}{2}$
解答 解:过点C作CG∥AB交BD的延长线于点G,
∴∠ABD=∠DGC,
∵BD、CE是ABC的两条中线,
∴BE=$\frac{1}{2}$AB,AD=CD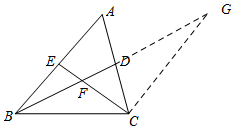
在△ABD与△CGD中,
$\left\{\begin{array}{l}{∠ABD=∠CGD}\\{∠ADB=∠CDG}\\{AD=CD}\end{array}\right.$
∴△ABD≌△CGD(AAS)
∴AB=CG,
∴BE=$\frac{1}{2}$CG,
∵BE∥CG,
∴△BEF∽△GCF,
∴$\frac{BE}{CG}=\frac{EF}{CF}$=$\frac{1}{2}$
点评 本题考查相似三角形的判定与性质,涉及全等三角形的判定与性质,三角形中线的性质,平行线的性质等知识,综合程度较高.

练习册系列答案
相关题目
18.某学校计划租用7辆客车送八年级师生去秋游,现有甲、乙两种型号客车,它们的载客量和租金如表,设租用甲种客车x辆.
(1)7辆客车载总人数为W,直接写出W(人)与x(辆)之间的函数关系式W=15x+210;
(2)租车总费用为y元.求出y(元)与x(辆)之间的函数关系式;指出自变量的取值范围;
(3)若该校八年级师生共有254名师生参加这次秋游,甲种客车不多于5辆,问:有几种可行的租车方案?哪种方案租车费最省?
| 甲种客车 | 乙种客车 | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 500 | 320 |
(2)租车总费用为y元.求出y(元)与x(辆)之间的函数关系式;指出自变量的取值范围;
(3)若该校八年级师生共有254名师生参加这次秋游,甲种客车不多于5辆,问:有几种可行的租车方案?哪种方案租车费最省?
8.与$\sqrt{30}$最接近的整数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
15.下列结论中,正确的是( )
| A. | 长度相等的两条弧是等弧 | B. | 相等的圆心角所对的弧相等 | ||
| C. | 平分弦的直径垂直于弦 | D. | 圆是中心对称图形 |
13.计算$\sqrt{{{({-3})}^2}}$的结果为( )
| A. | ±3 | B. | -3 | C. | 3 | D. | 9 |
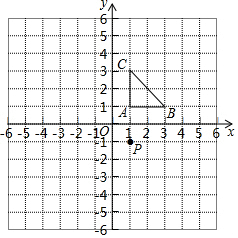 在平面直角坐标系中,小方格都是边长为1的正方形,△ABC≌△DEF,其中点A、B、C都在格点上,请你解答下列问题:
在平面直角坐标系中,小方格都是边长为1的正方形,△ABC≌△DEF,其中点A、B、C都在格点上,请你解答下列问题: 如图,已知∠β和线段a,c.
如图,已知∠β和线段a,c.