题目内容
17.解不等式组:$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x+1}{2}-1>x②}\end{array}\right.$,并在数轴上表示出不等式组的解集.分析 分别解两个不等式得到x>3和x>1,则利用同大取大可得到不等式组的解集,然后利用数轴表示解集.
解答 解:解①得x>3,
解②得x>1,
所以不等式组的解集为x>3,
用数轴表示为:
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,等边△ABC中,D是BC边上一点,BD=2DC,P是线段AD上的动点,过点P的直线交边AB、AC于点E、F,且∠APE=60°,则PE:PF=4:3.
如图,等边△ABC中,D是BC边上一点,BD=2DC,P是线段AD上的动点,过点P的直线交边AB、AC于点E、F,且∠APE=60°,则PE:PF=4:3.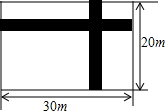 如图,在宽为20m,长为30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为500m2,若设路宽为x m,试计算路的宽度.
如图,在宽为20m,长为30m的矩形场地上,修筑同样宽的两条道路,余下的部分作为耕地,要使耕地的面积为500m2,若设路宽为x m,试计算路的宽度. 如图,直线a、b、c交于一点,d∥a.若∠1=130°,∠2=58°,求∠3的度数.
如图,直线a、b、c交于一点,d∥a.若∠1=130°,∠2=58°,求∠3的度数.