题目内容
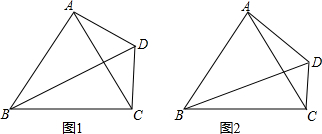
3. 如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线,求证:点D在线段AB的垂直平分线上.
如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线,求证:点D在线段AB的垂直平分线上.
分析 由在Rt△ABC中,∠C=90°,AB=2AC,可求得∠B=30°,∠BAC=60°,又由AD为∠BAC的平分线,可求得∠BAD=∠B,即可证得AD=BD,继而证得结论.
解答 证明:∵在Rt△ABC中,∠C=90°,AB=2AC,
∴∠B=30°,
∴∠BAC=90°-∠B=60°,
∵AD为∠BAC的平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴∠B=∠BAD,
∴AD=BD,
∴点D在线段AB的垂直平分线上.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的判定与性质.注意到线段两端点的距离相等的点在此线段的垂直平分线上.

练习册系列答案
相关题目
15.在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
12.无理数a满足:2<a<3,那么a可能是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | 2.5 | D. | $\frac{20}{7}$ |
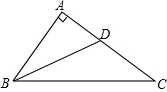 如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD=5.
如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD=5.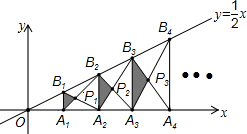 如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).
如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示). 如图,A点坐标为(-2,0),B点坐标为(0,-3).
如图,A点坐标为(-2,0),B点坐标为(0,-3).