题目内容
18. 如图,A点坐标为(-2,0),B点坐标为(0,-3).
如图,A点坐标为(-2,0),B点坐标为(0,-3).(1)作图:将△ABO沿x轴正方形平移4个单位,得到△DEF(其中A,B,O三点的对应点分别为D,E,F),延长ED交y轴于C点,过O点作OG⊥CE于点G;
(2)在(1)的条件下,求证:∠COG=∠EDF;
(3)求(1)的运动过程中线段AB扫过的图形的面积.
分析 (1)根据题意画出相应的图形,如图所示;
(2)利用同角的余角相等得到一对角相等,再利用对顶角相等,等量代换即可得证;
(3)运动过程中线段AB扫过的图形为平行四边形ABED,根据平移的距离及B的坐标求出AD与OB的长,即可求出运动过程中线段AB扫过的图形的面积.
解答  解:(1)做出相应的图形,如图所示;
解:(1)做出相应的图形,如图所示;
(2)∵OC⊥OD,OG⊥EC,
∴∠COG+∠DOG=90°,∠DOG+∠ODG=90°,
∴∠COG=∠ODG,
∵∠ODG=∠EDF,
∴∠COG=∠EDF;
(3)根据题意得:四边形ABED为平行四边形,且AD=BE=4,OB=3,
则运动过程中线段AB扫过的图形的面积S=S平行四边形ABED=AD•OB=12.
点评 此题属于一次函数综合题,涉及的知识有:平移的性质,平行四边形面积求法,坐标与图形性质,熟练掌握平移的性质是解本题第二问的关键.

练习册系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 同位角相等 | B. | 内错角相等 | C. | 同旁内角相等 | D. | 对顶角相等 |
9.为了实现道路畅通工程,我省今年计划公路建设累计投资92.7亿元,该数据用科学记数法可表示为( )
| A. | 9.27×109 | B. | 92.7×108 | C. | 9.27×1010 | D. | 0.927×1010 |
6.若分式$\frac{x-2}{x+1}$无意义,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
5.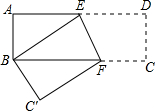 将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
 将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | $3\sqrt{3}$ |
 已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,求证:AD是BC的中垂线.
已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,求证:AD是BC的中垂线. 如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线,求证:点D在线段AB的垂直平分线上.
如图所示,在Rt△ABC中,∠C=90°,AB=2AC,AD为∠BAC的平分线,求证:点D在线段AB的垂直平分线上. 如图,在△ABC中,AD是∠BAC的角平分线,DE∥AB,DF∥AC,EF交AD于点O,试问DO是否是∠EDF的角平分线?请说明理由.
如图,在△ABC中,AD是∠BAC的角平分线,DE∥AB,DF∥AC,EF交AD于点O,试问DO是否是∠EDF的角平分线?请说明理由.