题目内容
5.已知点A在反比例函数y=$\frac{1}{x}$的图象上,点A、B关于原点O对称.(1)求证:点B在反比例函数y=$\frac{1}{x}$的图象上;
(2)若点C满足AC⊥x轴,BC⊥y轴,求证:△ABC的面积是定值.
分析 (1)设A(m,n),则mn=1,由于点A、B关于原点O对称,所以B(-m,-n),因为(-m)(-n)=1,可判定点B在反比例函数y=$\frac{1}{x}$的图象上;
(2)用m,n表示出AC、BC即可求出△ABC的面积.
解答 证明:(1)设A(m,n),则mn=1,
∵点A、B关于原点O对称,
∴B(-m,-n),
∵(-m)(-n)=1
∴点B在反比例函数y=$\frac{1}{x}$的图象上;
(2)由题意知C(m,-n),
则BC=2|m|,AC=2|n|,
△ABC的面积=$\frac{1}{2}BC•AC$=2|mn|=2mn=2,
∴△ABC的面积是定值.
点评 本题主要考查反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,三角形的面积,熟记反比例函数的性质是解题的关键.

练习册系列答案
相关题目
15.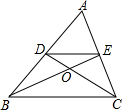 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )
 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△DCE=( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
16.湘西土家族苗族自治州6月2日至6月8日最高气温(℃)统计如下表:
则这七天最高气温的中位数为( )
| 日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
| 最高气温℃ | 28 | 25 | 25 | 30 | 32 | 28 | 27 |
| A. | 25℃ | B. | 27℃ | C. | 28℃ | D. | 30℃ |
13.一组数:8,9,7,10,6,9,9,6,则这组数的中位数与众数的和是( )
| A. | 16.5 | B. | 17 | C. | 17.5 | D. | 18 |
7.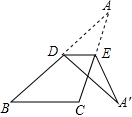 如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
 如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )
如图,在△ABC中,D,E分别是边AB,AC的中点,∠B=30°.现将△ADE沿DE折叠,点A落在三角形所在平面内的点为A′,则∠BDA′的度数为( )| A. | 100° | B. | 120° | C. | 130° | D. | 140° |