Question

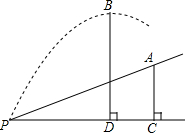如图，张强的叔叔在一次高尔夫球训练中，从山坡下P点打出一球向球洞A点飞去，球的飞行路线满足抛物线y=-

2 3

9

x²+4

3

x-6

3

，y（m）是球飞行的高度（相对于过P点的水平面），x（m）是球移动的水平距离．已知山坡PA与水平方向PC的夹角为30°，AC⊥PC于点C，P、A两点相距8

3

m，请你以P点为坐标原点，PC所在的直线为x轴，建立平面直角坐标系解决下列问题：
（1）点A的坐标

 

；
（2）求出球飞行时距离水平面的最大高度；
（3）判断张强的叔叔这一杆能否把高尔夫球从P点直接打进球洞A？如果能，请说明理由；如果不能，那么球应放在直线PC上的何处才能一次直接打入球洞A？

Answer 1

考点：二次函数综合题

专题：

分析：（1）根据已知条件求出AC，PC的长即可求出点A的坐标；
（2）根据抛物线的解析式即可求出球飞行时距离水平面的最大高度；
（3）不能把高尔夫球从P点直接打进球洞A，把点A的横坐标坐标打入y=-

2 3

9

x²+4

3

x-6

3

，计算y的值是否等于4

3

即可；设将抛物线沿PC平移h个单位，则新的抛物线解析式为：y=-

2 3

9

（x-9+h）²+18

3

，再把A的坐标代入求出h的值即可知道P平移的距离．

解答：解：（1）∵山坡PA与水平方向PC的夹角为30°，AC⊥PC于点C，P、A两点相距8

3

m，
∴AC=

1

2

AP=4

3

，
∴PC=

PA2-AC2

=12，
∴点A的坐标（12，4

3

），
故答案为：（12，4

3

）；
（2）∵原坐标原点O在以点P为原点的坐标系中的坐标为（0，6

3

），
∴原抛物线y=-

2 3

9

x²+4

3

x-6

3

在以p为坐标原点的坐标系中的解析式为：y=-

2 3

9

x²+4

3

x，
=-

2 3

9

（x-9）²+18

3

，
∴当x=9时，y_最大=18

3

米，
∴球飞行时距离水平面的最大高度是18

3

米；
（3）球不能直接打入球洞A，
理由如下：
∵点A的坐标（12，4

3

），
∴当x=12时，y=-

2 3

9

（12-9）²+18

3

=16

3

≠4

3

，
∴球不能直接打入球洞A，
若设将抛物线沿PC平移h个单位，则新的抛物线解析式为：
y=-

2 3

9

（x-9+h）²+18

3

，
∵点A的坐标（12，4

3

），
∴把x=12，打入y=-

2 3

9

（x-9+h）²+18

3

得：
4

3

=-

2 3

9

（x-9+h）²+18

3

，
解得：h=3

7

-3或-3

7

-3，
∵当h=-3

7

-3＜0，抛物线向右平移则点P在斜坡山应舍去，
当h=3

7

-3＞0，抛物线向左平移点P在抛物线上，
∴要想直接打入球洞A击球点P应向左平移（3

7

-3）米．

点评：本题考查了二次函数的应用及解直角三角形的知识，涉及了待定系数法求函数解析式的知识，注意建立数学模型，培养自己利用数学知识解决实际问题的能力，难度一般．