题目内容
 如图,已知Rt△ABC中,∠C=90°,∠BAC=67.5°,AD=BD,则sin∠ADC=( )
如图,已知Rt△ABC中,∠C=90°,∠BAC=67.5°,AD=BD,则sin∠ADC=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:特殊角的三角函数值,等腰三角形的性质
专题:
分析:先根据三角形内角和定理求出∠B的度数,再根据等腰三角形的性质求出∠BAD的度数,根据三角形外角的性质求出∠ADC的度数,由特殊角的三角函数值即可得出结论.
解答:解:∵Rt△ABC中,∠C=90°,∠BAC=67.5°,
∴∠B=90°-∠BAC=90°-67.5°=22.5°,
∵AD=BD,
∴∠B=∠BAD=22.5°,
∴∠ADC=∠B+∠BAD=22.5°+22.5°=45°,
∴sin∠ADC=sin45°=
.
故选B.
∴∠B=90°-∠BAC=90°-67.5°=22.5°,
∵AD=BD,
∴∠B=∠BAD=22.5°,
∴∠ADC=∠B+∠BAD=22.5°+22.5°=45°,
∴sin∠ADC=sin45°=
| ||
| 2 |
故选B.
点评:本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 教室里的饮水机接通电源就进入自动程序,开机加热每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.水温y(℃)和时间x(min)的关系如图.某天张老师在水温为30℃时,接通了电源,为了在上午课间时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
教室里的饮水机接通电源就进入自动程序,开机加热每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.水温y(℃)和时间x(min)的关系如图.某天张老师在水温为30℃时,接通了电源,为了在上午课间时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )| A、7:50 | B、7:45 |
| C、7:30 | D、7:20 |
下列运算正确的是( )
| A、a+2a=3a2 | ||||||
| B、a6÷a3=a2 | ||||||
C、
| ||||||
D、
|
2014年4月2日止,确认报考海南省公务员的人数达47263人,将47263用科学记数法表示为( )
| A、0.47263×105 |
| B、4.7263×104 |
| C、47.263×103 |
| D、472.63×102 |
不等式组
的解集为( )
|
| A、x>-1 | B、x>1 |
| C、无解 | D、-1<x<1 |
 如图,线段OA垂直射线OB于点O,OA=4,⊙A的半径是2,将OB绕点O沿顺时针方向旋转,当OB与⊙A相切时,OB旋转的角度为
如图,线段OA垂直射线OB于点O,OA=4,⊙A的半径是2,将OB绕点O沿顺时针方向旋转,当OB与⊙A相切时,OB旋转的角度为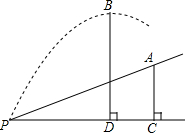 如图,张强的叔叔在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线满足抛物线y=-
如图,张强的叔叔在一次高尔夫球训练中,从山坡下P点打出一球向球洞A点飞去,球的飞行路线满足抛物线y=-