题目内容
3.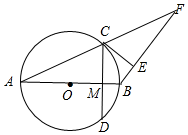 如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.
如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.(1)求证:AB=BF.
(2)求AF的长.
分析 (1)只要证明BC是线段AF的垂直平分线即可解决问题;
(2)由△ACM∽△CBM,可得CM2=AM•BM=16,求出CM,在Rt△ACM中,求出AC即可解决问题;
解答 (1)证明:连接 OC、BC.
OC、BC.
∵EC是⊙O的切线,
∴OC⊥EC,
∵BF⊥CE,
∴OC∥BF,
∵OA=BO,
∴AC=CF,
∵BA是直径,
∴∠ACB=90°,
∴BC⊥AF,
∴BA=BF.
(2)∵AB=10,OM:BM=3:2,
∴OM=3,BM=2,AM=8,
∵CM⊥AB,
易知△ACM∽△CBM,可得CM2=AM•BM=16,
∴CM=4,
在Rt△ACM中,AC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴AF=2AC=8$\sqrt{5}$.
点评 本题考查相似三角形的性质、勾股定理、垂径定理、线段的垂直平分线的性质、切线的性质等知识,解题的关键是学会添加常用辅助线,正确寻找相似三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.某班10名学生校服尺寸与对应人数如下表所示:
则这10名学生校服尺寸的中位数为170cm.
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
12.如图1~3,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图6中有6个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S6,则S1+S2+S3+…+S6的值是( )


| A. | π | B. | $\sqrt{2}$π | C. | 1.6π | D. | $\frac{3}{2}$π |
 如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)
如图,航拍无人机从点A处测得一幢建筑物顶部B的仰角为32°,测得底部C的仰角为62°,此时航拍无人机与该建筑物的水平距离AD为54米,求该建筑物的高度BC(精确到0.1米,参考数据:sin 32°=0.530,cos32°=0.848,tan32°=0.625,sin 62°=0.883,cos62°=0.469,tan62°=1.88)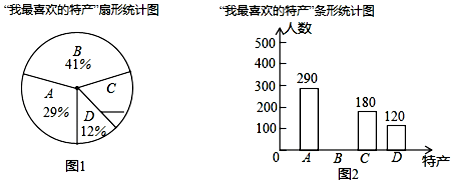
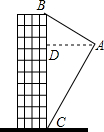
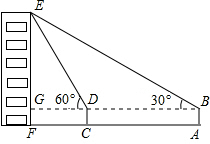 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)