题目内容
为了贯彻落实国家关于增强青少年体质的计划,我市全面实施了义务教育学段中小学学生“饮用奶计划”的营养工程.某牛奶供应商拟提供A(原味)、B(草莓味)、C(核桃味)、D(菠萝味)、E(香橙味)等五种口味的学生奶供学生选择(所有学生奶盒形状、大小相同),为了解对学生奶口味的喜好情况,某初级中学九年级(1)班张老师对全班同学进行了调查统计,制成了如图所示的两幅不完整的统计图.

(1)该班共有多少人?
(2)求出喜好A和C学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整;
(5)在进行调查统计的第二天,张老师为班上每位同学发放一盒学生奶.喜好B味的小明和喜好C味的小刚等四位同学最后领取,剩余的学生奶放在同一纸箱里,分别有B味2盒,C味和D味各1盒,张老师从该纸箱里随机取出两盒学生奶.请你用列表法或画树状图的方法,求出这两盒牛奶恰好同时是小明和小刚喜好的学生奶的概率.

(1)该班共有多少人?
(2)求出喜好A和C学生奶口味的人数;
(3)该班五种口味的学生奶喜好人数组成一组统计数据,求出这组数据的平均数;
(4)将折线统计图补充完整;
(5)在进行调查统计的第二天,张老师为班上每位同学发放一盒学生奶.喜好B味的小明和喜好C味的小刚等四位同学最后领取,剩余的学生奶放在同一纸箱里,分别有B味2盒,C味和D味各1盒,张老师从该纸箱里随机取出两盒学生奶.请你用列表法或画树状图的方法,求出这两盒牛奶恰好同时是小明和小刚喜好的学生奶的概率.
考点:折线统计图,扇形统计图,加权平均数,列表法与树状图法
专题:
分析:(1)根据喜欢B类型的人数及所占比例可得出学生总数;
(2)根据扇形统计图所给出的数据求出喜欢E类型的人数,再用总人数减去喜欢其它类型的人数,得出喜欢A的人数,再从条形统计图上可直接得出喜好C学生奶口味的人数;
(3)用总人数除以喜欢的五种类型,即可求出这组数据的平均数;
(4)根据(2)得出的数据可直接补图;
(5)设所剩学生奶分别用B1,B2,C,D表示,根据题意列出图表,再根据概率公式求出这两盒牛奶恰好同时是小明和小刚喜好的学生奶的概率即可.
(2)根据扇形统计图所给出的数据求出喜欢E类型的人数,再用总人数减去喜欢其它类型的人数,得出喜欢A的人数,再从条形统计图上可直接得出喜好C学生奶口味的人数;
(3)用总人数除以喜欢的五种类型,即可求出这组数据的平均数;
(4)根据(2)得出的数据可直接补图;
(5)设所剩学生奶分别用B1,B2,C,D表示,根据题意列出图表,再根据概率公式求出这两盒牛奶恰好同时是小明和小刚喜好的学生奶的概率即可.
解答:解:(1)根据题意得:
=40(人),
答:该班共有40人;
(2)喜欢E类型的人数是:40×15%=6人,则喜欢A类型的人数是40-12-8-10-6=4人,C学生奶口味的人数是8人;
(3)这组数据的平均数是40÷5=8;
(4)根据(2)得出的数据可直接补图,如下:

(5)设所剩学生奶分别用B1,B2,C,D表示,列表如下:
由表可知,一共有12种情况,其中恰好同时是小明和小刚喜好的学生奶(记为事件A)的共有4种结果:(B1,C),(B2,C),(C,B1),(C,B2),
则P(A)=
=
.则这两盒牛奶恰好同时是小明和小刚喜好的学生奶的概率为
.
| 12 |
| 30% |
答:该班共有40人;
(2)喜欢E类型的人数是:40×15%=6人,则喜欢A类型的人数是40-12-8-10-6=4人,C学生奶口味的人数是8人;
(3)这组数据的平均数是40÷5=8;
(4)根据(2)得出的数据可直接补图,如下:

(5)设所剩学生奶分别用B1,B2,C,D表示,列表如下:
| B1 | B2 | C | D | |
| B1 | (B1,B2) | (B1,C) | (B1,D) | |
| B2 | (B2,B1) | (B2,C) | (B2,D) | |
| C | (C,B1) | (C,B2) | (C,D) | |
| D | (D,B1) | (D,B2) | (D,C) |
则P(A)=
| 4 |
| 12 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了折线统和扇形统计图的知识,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,注意画出树状图或列表求概率.

练习册系列答案
相关题目
 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,AB=6cm,BC=8cm,则△AEF的周长是( )
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,AB=6cm,BC=8cm,则△AEF的周长是( )| A、14cm | B、8cm |
| C、9cm | D、10cm |
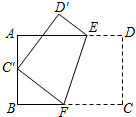 如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )| A、4 | ||
B、3
| ||
| C、4.5 | ||
| D、5 |
 如图,长方形纸片ABCD,点Q、E分别在AD,BC边上,将纸片折叠使点A落在点E处,折痕为PQ.若∠PEB=40°,则∠PQE=
如图,长方形纸片ABCD,点Q、E分别在AD,BC边上,将纸片折叠使点A落在点E处,折痕为PQ.若∠PEB=40°,则∠PQE=