题目内容
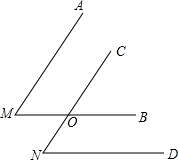 已知∠AMB和∠CND,且AM∥CN,BM∥DN,判断∠AMB与∠CND之间的数量关系.
已知∠AMB和∠CND,且AM∥CN,BM∥DN,判断∠AMB与∠CND之间的数量关系.(1)小明同学根据题意画出了如图的示意图,他得出的结论是∠AMB=∠CND,请你帮小明完成他的证明;
(2)小亮看了小明的结论后提出了异议,请你通过画图分析,表达你的观点和结论.(只需画图,并写出结论,不必证明).
考点:平行线的性质
专题:分类讨论
分析:(1)根据两直线平行,内错角相等可得∠AMB=∠MON,再根据两直线平行,内错角相等可得∠CND=∠MON,从而得解;
(2)再作出∠AMB是钝角时的情况,然后写出结论即可.
(2)再作出∠AMB是钝角时的情况,然后写出结论即可.
解答:
 解:(1)∵AM∥CN,
解:(1)∵AM∥CN,
∴∠AMB=∠MON,
∵BM∥DN,
∴∠CND=∠MON,
∴∠AMB=∠CND;
(2)如图,若∠AMB是钝角,则∠AMB+∠CND=180°,
所以,小明的结论错误,应该是∠AMB=∠CND或∠AMB+∠CND=180°.
 解:(1)∵AM∥CN,
解:(1)∵AM∥CN,∴∠AMB=∠MON,
∵BM∥DN,
∴∠CND=∠MON,
∴∠AMB=∠CND;
(2)如图,若∠AMB是钝角,则∠AMB+∠CND=180°,
所以,小明的结论错误,应该是∠AMB=∠CND或∠AMB+∠CND=180°.
点评:本题考查了平行线的性质,熟记性质是解题的关键,难点在于考虑两个角有一个角是钝角.

练习册系列答案
相关题目
将抛物线y=ax2-1(a≠0)的图象向左平移2个单位后,所得抛物线经过(1,-4)点,则a等于( )
A、-
| ||
| B、-1 | ||
| C、-3 | ||
| D、-5 |
若被除式是五次三项式,除式是三次单项式,则商式是( )
| A、五次三项式 |
| B、四次三项式 |
| C、三次三项式 |
| D、二次三项式 |
方程x2+3x-4=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、没有实数根 |
| C、有两个相等的实数根 |
| D、有一个实数根 |
 已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+
已知a,b,c三个数在数轴上的对应点如图所示,求|c-b|-|a-c|+ 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD.
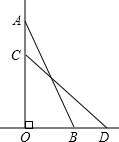 如图,一架25m的云梯AB斜靠在一竖直的墙AO上,这时AO为24m
如图,一架25m的云梯AB斜靠在一竖直的墙AO上,这时AO为24m